Question

In a triangle ABC, AB = 130, AC = 200 and BC = 260, point D is chosen on BC so that the circle inscribed in triangle ABD and ADC are tangent to AD at the same point, Length of BD is equal to.

$\left( A \right)105$
$\left( B \right)95$
$\left( C \right)90$
$\left( D \right)85$

Answer 1

Hint – In this particular question use the concept that according to circle tangent property the tangent drawn on the circle from the same point is always equal in length so use this concept to reach the solution of the question.

Complete step by step answer:
Given data:

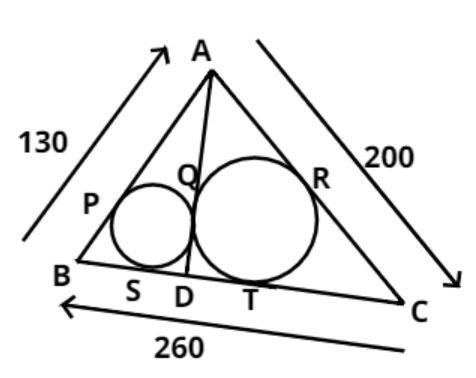
In a triangle ABC, AB = 130, AC = 200 and BC = 260 as shown in above figure.
And D is a point such that AD is a tangent to both the circles at the same point.
Let AB touch the smaller circle at point P, AD touch the smaller and bigger circle at same point which is Q, AC touch the bigger circle at point R, BC touch the smaller circle at point S and touch the bigger circle at point T as shown in the figure.
Now according to circle tangent property i.e. the tangent drawn on the circle from the same point is always equal in length.
Therefore, from point A tangent to smaller circle is AP and AQ
Therefore, AP = AQ.................... (1)
And from point A tangent to bigger circle is AP and AR
Therefore, AQ = AR................. (2)
Now from equation (1) and (2) we have,
AP = AQ = AR = x................... (3), where x is any positive real number
Similarly from point B, D and C we have,
BP = BS = y, where y is any positive real number
DS = DQ = DT = z, where z is any positive real number
And
CR = CT = n, where n is any positive real number
Now from figure, AP + BP = AB
                               BS + DS + DT + CT = BC
                               AR + CR = AC
Now substitute the values in the above equations we have,
$ \Rightarrow x + y = 130$................... (4)
$y + z + z + n = 260$................. (5)
$x + n = 200$.................... (6)
Now we have to find the value of BD, so from the figure, BD = BS + DS
Therefore, BD = y + z................ (7)
Now add equation (4), (5) and (6) we have,
$ \Rightarrow x + y + y + z + z + n + x + n = 130 + 260 + 200$
Now simplify this we have,
$ \Rightarrow 2x + 2y + 2z + 2n = 590$
Now divide by 2 throughout we have,
$ \Rightarrow x + y + z + n = \dfrac{{590}}{2} = 295$
Now subtract equation (6) from the above equation we have,
$ \Rightarrow x + y + z + n - x - n = 295 - 200$
$ \Rightarrow y + z = 95$
Now from equation (7) we have,
BD = 95
So this is the required answer.
Hence option (B) is the correct answer.

Note – Whenever we face such types of question the key concept we have to remember is that always recall the circle tangent property from a fixed point which is stated above then write the equations using this property as above and simplify we will get the required length of the BD which is the required answer.