
In a triangle ABC $a=7,b=8,c=9$ BD is the median and BE is the altitude from vertex B then
List-I List-II A) BD 1. $7$ B) BE 2. $2$ C) ED 3. $\sqrt{35}$ 4. $\sqrt{45}$
A) A-2, B-1, C-4
B) A-3, B-4, C-2
C) A-1, B-3, C-2
D) A-1 ,B-4,C-2
| List-I | List-II |
| A) BD | 1. $7$ |
| B) BE | 2. $2$ |
| C) ED | 3. $\sqrt{35}$ |
| 4. $\sqrt{45}$ |
Answer
532.8k+ views
Hint: The altitude of a triangle meets the side of the triangle such that the angle at which it meets the triangle is ${{90}^{\circ }}$.
The median of a triangle bisects the sides of the triangle.
We can use the formula for $\sin \theta ,\cos \theta $.
Complete step by step solution:
For a triangle ABC, BD is median and BE is altitude the sides of triangle are $a=7,b=8,c=9$
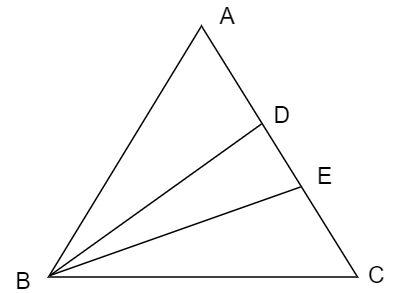
AC=4
Since BD is the median which bisects the side of triangle AD=4
Consider $\Delta ABD$
$\begin{align}
& AD=b \\
& c=9 \\
& a=BD \\
\end{align}$
Now for a triangle the formula of $\cos A$ is given by:
$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Substitute all the value of a,b,c in equation above we get:
$\cos A=\dfrac{{{4}^{2}}+{{9}^{2}}-B{{D}^{2}}}{2\times 4\times 9}$ …..(1)
Now from triangle ABC we have,
$\cos A=\dfrac{{{8}^{2}}+{{9}^{2}}-{{7}^{2}}}{2\times 8\times 9}$ …..(2)
Equating equation (1) and (2) we get,
$\dfrac{{{4}^{2}}+{{9}^{2}}-B{{D}^{2}}}{2\times 4\times 9}$$=\dfrac{{{8}^{2}}+{{9}^{2}}-{{7}^{2}}}{2\times 8\times 9}$
Cancel the common terms from L.H.S and R.H.S and solve:
$\begin{align}
& 2\left( 16+81-B{{D}^{2}} \right)=64+81-49 \\
& \Rightarrow 32+162-2B{{D}^{2}}=96 \\
& \Rightarrow B{{D}^{2}}=49 \\
& \therefore BD=7 \\
\end{align}$
Thus, from list-I option A the correct choice is (2).
Since $BD=BC=7$ therefore the $\Delta BCD$ is an isosceles triangle.
Therefore, the line bisects the side CD into two equal parts.
Hence, we can conclude that
$\begin{align}
& ED=EC \\
& \Rightarrow ED=\dfrac{CD}{2} \\
& \therefore ED=2 \\
\end{align}$
Hence the correct match for option (C) is (1)
To find BE use $\Delta BEC$ which is a right-angled triangle.
From Pythagoras theorem we have
${{H}^{2}}={{P}^{2}}+{{B}^{2}}$
$\begin{align}
& B{{C}^{2}}=E{{C}^{2}}+B{{E}^{2}} \\
& \Rightarrow BE=\sqrt{{{7}^{2}}-{{2}^{2}}} \\
& \Rightarrow BE=\sqrt{49-4} \\
& \therefore BE=\sqrt{45} \\
\end{align}$
The correct match for option (B) is (3)
To find AE:
$\begin{align}
& AC=AE+EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=8-2 \\
& \therefore AE=6 \\
\end{align}$
So, the correct answer is “Option D”.
Note: This question can be solved by using the properties of triangle do keep in mind the definition of altitude and median to avoid confusion and make use of it to solve the question as a median bisects the side of triangle while altitude makes ${{90}^{\circ }}$ at the side.
The median of a triangle bisects the sides of the triangle.
We can use the formula for $\sin \theta ,\cos \theta $.
Complete step by step solution:
For a triangle ABC, BD is median and BE is altitude the sides of triangle are $a=7,b=8,c=9$

AC=4
Since BD is the median which bisects the side of triangle AD=4
Consider $\Delta ABD$
$\begin{align}
& AD=b \\
& c=9 \\
& a=BD \\
\end{align}$
Now for a triangle the formula of $\cos A$ is given by:
$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Substitute all the value of a,b,c in equation above we get:
$\cos A=\dfrac{{{4}^{2}}+{{9}^{2}}-B{{D}^{2}}}{2\times 4\times 9}$ …..(1)
Now from triangle ABC we have,
$\cos A=\dfrac{{{8}^{2}}+{{9}^{2}}-{{7}^{2}}}{2\times 8\times 9}$ …..(2)
Equating equation (1) and (2) we get,
$\dfrac{{{4}^{2}}+{{9}^{2}}-B{{D}^{2}}}{2\times 4\times 9}$$=\dfrac{{{8}^{2}}+{{9}^{2}}-{{7}^{2}}}{2\times 8\times 9}$
Cancel the common terms from L.H.S and R.H.S and solve:
$\begin{align}
& 2\left( 16+81-B{{D}^{2}} \right)=64+81-49 \\
& \Rightarrow 32+162-2B{{D}^{2}}=96 \\
& \Rightarrow B{{D}^{2}}=49 \\
& \therefore BD=7 \\
\end{align}$
Thus, from list-I option A the correct choice is (2).
Since $BD=BC=7$ therefore the $\Delta BCD$ is an isosceles triangle.
Therefore, the line bisects the side CD into two equal parts.
Hence, we can conclude that
$\begin{align}
& ED=EC \\
& \Rightarrow ED=\dfrac{CD}{2} \\
& \therefore ED=2 \\
\end{align}$
Hence the correct match for option (C) is (1)
To find BE use $\Delta BEC$ which is a right-angled triangle.
From Pythagoras theorem we have
${{H}^{2}}={{P}^{2}}+{{B}^{2}}$
$\begin{align}
& B{{C}^{2}}=E{{C}^{2}}+B{{E}^{2}} \\
& \Rightarrow BE=\sqrt{{{7}^{2}}-{{2}^{2}}} \\
& \Rightarrow BE=\sqrt{49-4} \\
& \therefore BE=\sqrt{45} \\
\end{align}$
The correct match for option (B) is (3)
To find AE:
$\begin{align}
& AC=AE+EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=AC-EC \\
& \Rightarrow AE=8-2 \\
& \therefore AE=6 \\
\end{align}$
So, the correct answer is “Option D”.
Note: This question can be solved by using the properties of triangle do keep in mind the definition of altitude and median to avoid confusion and make use of it to solve the question as a median bisects the side of triangle while altitude makes ${{90}^{\circ }}$ at the side.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




