Question

In a triangle, ABC, a = 7, b = 5, c = 3. \[{{p}_{1}},{{p}_{2}},{{p}_{3}}\] are the altitudes from A, B, C. Then find the last digit of \[4{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}\].

Answer 1

Hint: First of all, find the area of the triangle by Heron’s formula that is \[\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]. Now, also find the value of the area of the triangle by \[\dfrac{1}{2}\] base \[\times \] height. Equate these two values to find the value of \[a{{p}_{1}},b{{p}_{2}}\] and \[c{{p}_{3}}\]. From this, find the required value of the given expression.

Complete step-by-step answer:
Here, we are given a triangle ABC in which a = 7, b = 5, c = 3 and \[{{p}_{1}},{{p}_{2}},{{p}_{3}}\] are the altitudes from A, B, and C. We have to find the last digit of \[4{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}\]. Let us draw a triangle ABC with a = 7, b = 5 and c = 3.

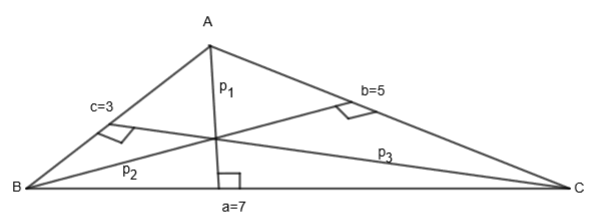
In the above triangle ABC, \[{{p}_{1}},{{p}_{2}},{{p}_{3}}\] are the altitudes from A, B, and C respectively. We know that by Heron’s formula, we get,
\[\text{Area of }\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]
where a, b and c are the sides of the triangle and \[s=\dfrac{a+b+c}{2}\].
So, by substituting a = 7, b = 5, c = 3, we get,
\[s=\dfrac{7+5+3}{2}=\dfrac{15}{2}\]
So, we get the area of \[\Delta ABC\] as,
\[\text{Area of }\Delta ABC=\sqrt{\left( \dfrac{15}{2} \right)\left( \dfrac{15}{2}-7 \right)\left( \dfrac{15}{2}-5 \right)\left( \dfrac{15}{2}-3 \right)}\]
\[\text{Area of }\Delta ABC=\sqrt{\left( \dfrac{15}{2} \right)\left( \dfrac{1}{2} \right)\left( \dfrac{5}{2} \right)\left( \dfrac{9}{2} \right)}\]
\[\text{Area of }\Delta ABC=\sqrt{\dfrac{225\times 3}{16}}\]
\[\text{Area of }\Delta ABC=\dfrac{15\sqrt{3}}{4}sq.units.....\left( i \right)\]
Now, we also know that area of the triangle \[=\dfrac{1}{2}\times base\times height\].
So, from this, we get the area of the triangle \[=\dfrac{1}{2}{{p}_{1}}.BC=\dfrac{1}{2}{{p}_{2}}.AC=\dfrac{1}{2}{{p}_{3}}.AB\]
Area of \[\Delta ABC=\dfrac{1}{2}{{p}_{1}}a=\dfrac{1}{2}{{p}_{2}}b=\dfrac{1}{2}{{p}_{3}}c....\left( ii \right)\]
So, by equating the area of the triangle ABC from equation (i) and (ii), we get,
\[\dfrac{1}{2}a{{p}_{1}}=\dfrac{1}{2}b{{p}_{2}}=\dfrac{1}{2}c{{p}_{3}}=\dfrac{15\sqrt{3}}{4}\]
By multiplying 2 on both the sides of the above equation, we get,
\[a{{p}_{1}}=b{{p}_{2}}=c{{p}_{3}}=\dfrac{15\sqrt{3}}{4}.2\]
\[a{{p}_{1}}=b{{p}_{2}}=c{{p}_{3}}=\dfrac{15\sqrt{3}}{2}\]
So, we get,
\[a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}}=\dfrac{15\sqrt{3}}{2}+\dfrac{15\sqrt{3}}{2}+\dfrac{15\sqrt{3}}{2}\]
\[a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}}=3\times \dfrac{15\sqrt{3}}{2}\]
\[a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}}=\dfrac{45\sqrt{3}}{2}\]
By squaring both the sides of the above equation, we get,
\[{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}={{\left( \dfrac{45\sqrt{3}}{2} \right)}^{2}}\]
\[{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}={{\left( 45 \right)}^{2}}.\dfrac{3}{4}\]
By multiplying 4 on both the sides of the above equation, we get,
\[4{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}=6075\]
So, we get the last digit of expression \[4{{\left( a{{p}_{1}}+b{{p}_{2}}+c{{p}_{3}} \right)}^{2}}\] as 5.

Note: In these types of questions, students must draw the diagram to visualize the question. Students must note that in a triangle, any sides can be taken as the base of the triangle but only the corresponding height should be taken to calculate the area of the triangle. Also, students must remember the various formulas for finding the area of the triangle as they are very useful in geometry while solving the questions related to the triangle.