Question

In a trapezium ABCD if E and F be the mid-point of the diagonals AC and BD respectively, then EF =
(A) \[\dfrac{1}{2}AB\]
(B) \[\dfrac{1}{2}CD\]
(C) \[\dfrac{1}{2}\left( AB+CD \right)\]
(D) \[\dfrac{1}{2}\left( AB-CD \right)\]

Answer 1

Hint: We are given a question based on trapezium and we have to find the equivalent, we will be using the properties of a trapezium to find the required and most appropriate answer from the given options. Firstly, we will draw the figure as per the given and then we will find the length of the EF in terms of AB and CD only. Hence, we will have the required value.

Complete step by step answer:
According to the given question, we are given a trapezium ABCD and we have to find the equivalent of EF in terms of AB and CD from the given options.
As per the question, we have the figure as,

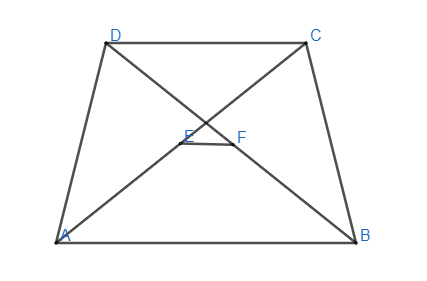
We will now assume a point on the side AB, such that the line through the point C and F touches the side AB on point G. we have the figure as,

We will now consider the triangles, \[\vartriangle CDF\] and \[\vartriangle GBF\]
\[DF=BF\] (Since F is the mid-point of the diagonal BD)
\[\angle DCF=\angle BGF\] (Since \[AB||CD\] and so we have \[GB||CD\] so the alternate angles or transverse angles are equal)
\[\angle CDF=\angle GBF\] (Since \[AB||CD\] and so we have \[GB||CD\] so the alternate angles or transverse angles are equal)
Therefore, \[\vartriangle CDF\cong \vartriangle GBF\] (by ASA (Angle - Side – Angle) congruence rule)
So, we have, \[CD=GB\] (by C.P.C.T)
We can see that in \[\vartriangle CAG\], E and F are the mid-points of the side AC and CG, and so we can write that,
\[EF=\dfrac{1}{2}\left( AG \right)\]
Also, we can write AG as,
\[\Rightarrow EF=\dfrac{1}{2}\left( AB-BG \right)\]
From the above congruence, we found \[CD=GB\], so we get,
\[\Rightarrow EF=\dfrac{1}{2}\left( AB-CD \right)\]
So, the correct answer is “Option D”.

Note: The congruence rule applicable should be written and not left out else the congruency of the two triangles cannot be established. Also, the diagram should be clearly made as it helps in the solving of the given question more vividly. Also, do not skip steps and write the solution stepwise without any errors.