Question

In a third class of lever, the effort arm is $10\,cm$ and load is given at a distance $500\,cm$ away from the effort on the opposite side of the fulcrum. Find the mechanical advantage?

A. $M.A = \dfrac{{10}}{{51}}$
B.$M.A = \dfrac{1}{{58}}$
C.$M.A = \dfrac{2}{{51}}$
D.$M.A = \dfrac{1}{{51}}$

Answer 1

Hint-
Mechanical advantage is the ratio of the force produced by a machine to the force applied to for assessing the performance of a machine.
It can be written as
$MA = \dfrac{{Effort\,arm}}{{load\,arm}}$
The distance from the applied force, also known as effort force to the fulcrum is called the effort or input arm and the distance from the load to the fulcrum is called the load or output arm.

Step by step solution:
Mechanical advantage is the ratio of the force produced by a machine to the force applied to for assessing the performance of a machine.
It can be written as
$MA = \dfrac{{Effort\,arm}}{{load\,arm}}$
The arm of a force relative to a given point is the shortest distance from the point to the line of action of the force or it can be said as the length of the perpendicular from the point to the line of action of the force.
The distance from the applied force, also known as effort force to the fulcrum is called the effort or input arm and the distance from the load to the fulcrum is called the load or output arm.
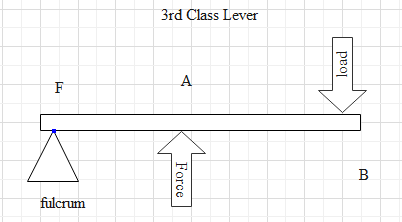
Fulcrum is the pivot point about which lever turns.
In the question it is given that,
$effort\,arm = 10\,cm$
 And load is at a distance $500\,cm$ away from the effort on the opposite side of the fulcrum.
let this be denoted as $d$
$d = 500\,cm$
But we need distance from the fulcrum to the line of action of force
Therefore, effort arm
$
  load\,arm = effort\,arm + d \\
   = 10\,cm + 500\,cm \\
   = 510\,cm \\
 $
Now mechanical advantage can be calculated as
$
  MA = \dfrac{{Effort\,arm}}{{load\,arm}} \\
   = \dfrac{{10\,cm}}{{510\,cm}} \\
   = \dfrac{1}{{51}} \\
 $

So, the correct answer is option D

Note: Here, it is given that the lever is a third-class lever. In a third class lever the fulcrum will be at one end of the lever and force acting in the middle load will be placed at the other end. Since in the question the effort arm is given, that will give us the distance from the fulcrum to the line of application of force. To find the load arm, the distance between force and the load is given. Since, load arm is the distance from fulcrum to the load, be careful to add both to get the actual load arm distance.