Question

In a survey of\[{\text{600}}\] students in a school, \[{\text{150}}\] students were found to be taking tea and \[{\text{225}}\] taking coffee, \[{\text{100}}\] were taking both tea and coffee. Find how many students were taking neither tea nor coffee?

Answer 1

Hint: - Divide the given numbers into separate categories using a venn diagram and try to get the total number of students who are actually taking tea and coffee so that we can subtract them from total.

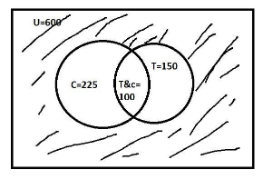
Let ${\text{U}}$ be the set of all students who took part in the survey.
Let ${\text{T}}$ be the set of students taking tea.
Let ${\text{C}}$ be the set of students taking coffee.
Now write these in the form of set,
$n(U) = 600,n(T) = 150,n(C) = 225,$
${\text{100}}$ Were taking both tea and coffee means $n(T \cap C) = 100$
To find Number of student taking neither tea nor coffee
I.e. we have to find$n(T' \cap C')$.
 Here ${\text{T'}}$and ${\text{C'}}$ means not taking tea and coffee.
 It means a total number of students$ - $either taking tea or coffee.

$ \Rightarrow n(T' \cap C'{\text{) = }}n(T \cup C)'$

 And by set formula we know that $n(T \cup C) = [n(T) + n(C) - n(T \cap C)]$
$ = n(U) - n(T \cup C) \\
   = n(U) - [n(T) + n(C) - n(T \cap C)] \\
   = 600 - [150 + 225 - 100] \\
   = 600 - 275 \\
   = 325 \\
$
Hence, ${\text{325}}$ students were taking neither tea nor coffee.

Note: - whenever we face such a type of question, we have to apply the property set for solving the question and we also make a venn diagram for easy solving. Here in this venn diagram you have to find the shaded region.