Question

In a survey of $ 100 $ students the number of students studying various languages is found as: English only $ 18 $ ; English but not Hindi $ 23 $ ; English and Sanskrit $ 8 $ ; Sanskrit and Hindi $ 8 $ ; English $ 26 $ ; Sanskrit $ 48 $ and no language $ 24 $ . Find
1) How many students are studying Hindi?
2) How many students are studying both English and Hindi?

Answer 1

Hint: First of all we draw three Venn diagrams. One for subject English, one for subject Hindi and one for subject Sanskrit. Then we name different regions of the Venn diagram with letters a, b, c, d,…… and so on as many required and then framing equations as per given conditions to solve values of a, b, c, d,….. Or either relation between them to get the required option.

Complete step-by-step answer:
To find a solution to this type of problem we choose the Venn diagram method of set theory.
Let Students who study English language denoted by set E, those who study Hindi language denoted by set H and those who study Sanskrit denoted by set S.
Now, draw a Venn diagram of three subjects and give names to different regions formed as shown in figure.

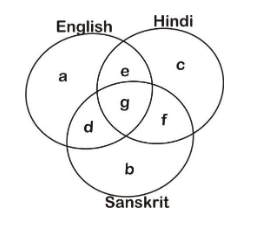
From statement we have
Total number of students = $ 100 $
Only English = $ 18 $ or using Venn diagram we have an equation for only English: a = $ 18 $
English but not Hindi = $ 23 $
Writing above according to Venn diagram we have a + d = $ 23 $
But as we knows the value of ‘a’ so, using a= $ 18 $ in above to get value of d
 $
  18 + d = 23 \\
   \Rightarrow d = 23 - 18 \\
   \Rightarrow d = 5 \\
  $
English and Sanskrit = $ 8 $
Witting according to Venn diagram we have g + d = $ 8 $
But as we have calculated the value of d = $ 5 $ in above set. So, using it to find the value of b.
 $
  g + 5 = 8 \\
   \Rightarrow g = 8 - 5 \\
   \Rightarrow g = 3 \\
  $
Sanskrit and Hindi = $ 8 $
Writing above according to Venn diagram we have f + g = $ 8 $
But as we have calculated the value of g = $ 3 $ in above. So, using it to find the value of f.
 $
  f + 3 = 8 \\
   \Rightarrow f = 8 - 3 \\
   \Rightarrow f = 5 \\
  $
English = $ 26 $
Writing above according to Venn diagram we have a + e + d + g = $ 26 $
Using, values of a, d, and g calculated above we find value of ‘e’
 $ 18 + e + 5 + 3 = 26 $
 $
  26 + e = 26 \\
   \Rightarrow e = 0 \\
  $
Sanskrit = $ 48 $
Writing above according to Venn diagram we have d + b + g + f = $ 48 $
Using values of g, f and d calculated above we find the value of b.
 $
  b + 5 + 3 + 5 = 48 \\
   \Rightarrow b + 13 = 48 \\
   \Rightarrow b = 48 - 15 \\
   \Rightarrow b = 35 \\
  $
Since, it is given that the total number of students are $ 100 $ and there are $ 24 $ students who don’t study any language.
Therefore, we can calculate the number of students who study at least one language by calculating the difference between the total number of students and those who don’t study any language.
Number of students study at least one language = $ 100 - 24 = 76 $
Using this in the form of a Venn diagram. We have;
a + b + c + d + e + f + g = $ 76 $
Using values of a, b, d, e, f and g calculated above to find the value of c.
 $
  18 + 35 + c + 5 + 0 + 5 + 3 = 76 \\
   \Rightarrow c + 66 = 76 \\
   \Rightarrow c = 76 - 66 \\
   \Rightarrow c = 10 \\
  $
Hence, from above we see that we have calculated values of each region of Venn diagram.
Now, using this we answer given problem

So, number of students studying Hindi using Venn diagram given as
c + e + g + f
Now, substituting their values as calculated above. We have;
 $
  10 + 3 + 5 + 0 \\
   = 18 \\
  $
Hence, number of students who study Hindi are $ 18 $
Also, for part 2.) we have to calculate how many students are studying Hindi and English both.
According to Venn diagram it is given as
g + e
Using values of g and e calculated above. We have;
 $
  3 + 0 \\
   = 3 \\
  $
Hence, the number of students who study Hindi and English both are 3.

Note: This type of problems can also be solved by using set theory formulas. If we apply a formula method to solve these problems then we have to remember or use a number of formulas which make it difficult as compared to the Venn diagram method. But solving it by using a Venn diagram is more convenient as it doesn't require much formulas and one can understand the solution of the problem very easily.