Question

In a survey of $100$ people, \[36\% \] like movie A, 39% like movie B, \[41\% \] like movie C, \[6\% \] like both A & B, \[8\% \] like both B & C, \[7\% \] like both A & C and \[3\% \] like none of the three. Find how many people like
$\left( i \right)$ All the three movies
$\left( {ii} \right)$ Exactly two movies

Answer 1

Hint: We can use the basic formula of three sets in the given problems to find the solution. To find the solution for how many people like all the three movies, we have to find $n(A \cap B \cap C)$. To find the solution for how many people like exactly two movies, we can use a formula.

Formula used: $n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(A \cap C) + n(A \cap B \cap C)$
$n\left( {exactly{\text{ }}two{\text{ }}sets} \right) = n\left( {A \cap B} \right) + n\left( {B \cap C} \right) + n(C \cap A) - 3n(A \cap B \cap C)$

Complete step-by-step solution:
Here we have to find,
$\left( i \right)$ All the three movies
Let us construct a set diagram from the given information.

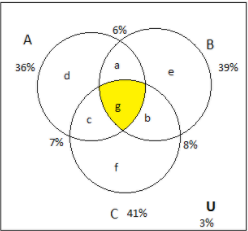
Here, $g$ is the number of people who like all the three movies. (i.e.) $n(A \cap B \cap C)$
It is a survey of $100$ people and we have $100\% $, therefore each percentage denotes a single person.
$\therefore n(U) = 100$
Similarly, we write the given data as follows:
$n(A) = 36$
$n(B) = 39$
$n(C) = 41$
$n(A \cap B) = 6$
$n(B \cap C) = 8$
$n(A \cap C) = 7$
$n(A \cup B \cup C)' = 3$ which gives $n(A \cup B \cup C) = U - n(A \cup B \cup C)'$
$\therefore n(A \cup B \cup C) = 100 - 3 = 97$
We can use the formula of three sets
$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(A \cap C) + n(A \cap B \cap C)$
Here, we need $n(A \cap B \cap C)$, so we can rewrite the formula as
$n(A \cap B \cap C) = n(A \cup B \cup C) - n(A) - n(B) - n(C) + n(A \cap B) + n(B \cap C) + n(A \cap C)$
On putting the values we get,
$n(A \cap B \cap C) = 97 - 36 - 39 - 41 + 6 + 8 + 7$
On simplifying we get,
$\therefore n(A \cap B \cap C) = 2$
Therefore, the number of people who like all the three movies are 2.
$\left( {ii} \right)$ Exactly two movies
Now, we need the total value of a, b and c.

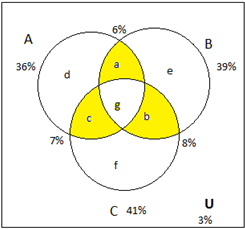
The formula to find exactly two sets is
$n\left( {exactly{\text{ }}two{\text{ }}sets} \right) = n\left( {A \cap B} \right) + n\left( {B \cap C} \right) + n(C \cap A) - 3n(A \cap B \cap C)$
Putting the values and we get,
$ = 6 + 8 + 7 - 3(2)$
Let us add the term and multiply the second term we get,
$ \Rightarrow 21 - 6$
On subtract we get,
$ \Rightarrow 15$

Therefore, the number of people who liked exactly two movies is 15

Note: In this question we have an alternative method for exactly two sets as follows:
We have to add the values of those who like both movies A and B, B and C & A and C after subtracting by those who like all the three movies.
(i.e.) we can write it as mathematically we get, $a = n(A \cap B) - n(A \cap B \cap C)$
$a = 6 - 2 = 4$
Similarly, $b = 8 - 2 = 6$ and $c = 7 - 2 = 5$
By adding a, b and c= $4 + 6 + 5 = 15$
Therefore, the number of people who liked exactly two movies is $15$.