Question

In a survey it was found that 21 persons liked product ${{P}_{1}}$, 26 liked product ${{P}_{2}}$, and 29 persons liked product ${{P}_{3}}$. If 14 persons liked products ${{P}_{1}}$ and ${{P}_{2}}$; 12 persons liked ${{P}_{3}}$ and ${{P}_{1}}$; 14 persons liked ${{P}_{2}}$ and ${{P}_{3}}$ and 8 liked all the three products. Find out how many liked product ${{P}_{3}}$ only.

Answer 1

Hint: In this question, we will use a Venn diagram to find the correct answer, because it will give a proper visualisation. Then we can form equations using the number of persons in sets ${{P}_{1}},{{P}_{2}},{{P}_{3}}$ given in the question. For example, we have been given that 8 liked all the three products, so it denotes the intersection of all the sets and the corresponding number in the Venn diagram can be equated to 8. Then, using this, we can find all other numbers of persons in each condition.

Complete step-by-step answer:
In this question, we are asked to find the number of persons who liked the product ${{P}_{3}}$ only. So, for that, we will use the Venn diagram, which is represented as follows with the inputs given in the question.

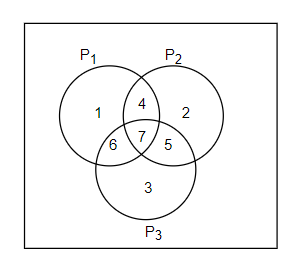
As you can see, here, we have considered each group by a number. The persons who liked ${{P}_{1}}$ as 1, persons who liked ${{P}_{2}}$ as 2, persons who liked ${{P}_{3}}$ as 3, persons who liked ${{P}_{1}}$ and ${{P}_{2}}$ but not ${{P}_{3}}$ as 4, persons who liked ${{P}_{2}}$ and ${{P}_{3}}$ but not ${{P}_{1}}$ as 5, persons who liked ${{P}_{3}}$ and ${{P}_{1}}$ but not ${{P}_{2}}$ as 6 and persons who liked all three of them as 7. Now, we have been given that 21 persons liked product ${{P}_{1}}$, so according to the Venn diagram, we can write it as,
n (1) + n (4) + n (6) + n (7) = 21 ……… (i)
Similarly, 26 liked product ${{P}_{2}}$, so we get,
n (2) + n (4) + n (5) + n (7) = 26 ……… (ii)
And 29 persons liked product ${{P}_{3}}$, so we can write,
n (3) + n (5) + n (6) + n (7) = 29 ……… (iii)
Now, 14 persons liked products ${{P}_{1}}$ and ${{P}_{2}}$, so we get,
n (4) + n (7) = 14 ……… (iv)
And, 12 persons liked ${{P}_{3}}$ and ${{P}_{1}}$, so we get,
n (6) + n (7) = 12 ……… (v)
And, 14 persons liked ${{P}_{2}}$ and ${{P}_{3}}$, so we get,
n (5) + n (7) = 14 ……… (vi)
And, finally 8 liked all the three products, so we get,
n (7) = 8 ……… (vii)
Now, we will put the values of n (7) from equation (vii) in equation (vi). So we get,
n (5) + 8 = 14
n (5) = 6 ……… (viii)
Now, we will put the value of n (7) in equation (v). So, we get,
n (6) + 8 = 12
n (6) = 4 ……… (ix)
Now, according to the question, we have to find the value of n (3). For that we will put the values of n (5), n (6) and n (7) from equations (viii), (ix) and (vii) in equation (iii). So, we get,
n (3) + 6 + 4 + 8 = 29
n (3) = 29 - 18
so, n (3) = 11.
Hence, we can say that there are 11 persons who liked only the product ${{P}_{3}}$.

Note: While solving this question, there is a high possibility that we make mistakes in calculations. Also, we can solve this question by using the formula $n\left( only\text{ }{{P}_{3}} \right)=n\left( {{P}_{3}} \right)-n\left( {{P}_{1}}\cap {{P}_{3}} \right)-n\left( {{P}_{2}}\cap {{P}_{3}} \right)+n\left( {{P}_{1}}\cap {{P}_{2}}\cap {{P}_{3}} \right)$, but we may not remember the formula always.