Question

In a square cut, the speed of cricket ball changes from $ 30m{s^{ - 1}} $ to $ 40m{s^{ - 1}} $ during the time of its contact $ \Delta t = 0.01s $ with the bat. If the ball is deflected by the bat through an angle of $ \theta = 90^\circ $ , find the magnitude of the average acceleration (in $ \times {10^2}m{s^{ - 2}} $ ) of the ball during the square cut.

Answer 1

Hint: Although acceleration is nothing but change in velocity per unit time, here we can see that there will be a change in direction clearly along with the change in magnitude. So, we should be seeing the velocity as a vector quantity and not a scalar quantity.

Formulas used We will be using the formula $ a = \dfrac{{{v_2} - {v_1}}}{{\Delta t}} $ where $ {v_1} $ is the initial velocity, $ {v_2} $ is the final velocity, and $ \Delta t $ is the time taken to cause the change in velocity from $ {v_1} $ to $ {v_2} $ . Also we will be using the formula $ \left| {\overrightarrow {\Delta v} } \right| = \sqrt {(v_1^2 + v_2^2 - 2{v_1}{v_2}\cos \theta )} $ where $ \theta $ is the angle of deflection between the final and initial velocities.

Complete Answer:
We know that the acceleration of a body is the rate of change of velocity of that body, but we also know that the velocity is a vector quantity and not a scalar quantity. So, the velocity as a vector has both magnitude and direction.
Here the velocity vector approaches the surfaces of the bat and then leaves the bat at a different magnitude of velocity and an angle of deflection $ \theta = 90^\circ $ .

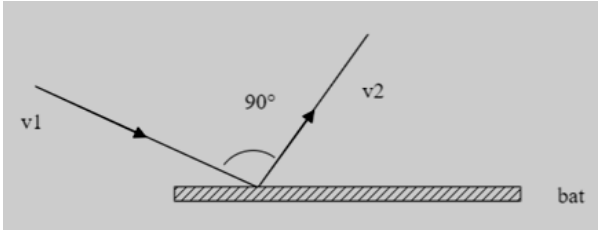
So, the resultant of this velocity vector $ \overrightarrow v $ will be $ \left| {\overrightarrow {\Delta v} } \right| = \sqrt {(v_1^2 + v_2^2 - 2{v_1}{v_2}\cos \theta )} $ . Substituting the values of $ {v_1} = 30m/s $ , $ {v_2} = 40m/s $ and $ \theta = 90^\circ $ we get. $ \left| {\overrightarrow {\Delta v} } \right| = \sqrt {({{(30)}^2} + {{(40)}^2} - 2(30)(40)\cos 90^\circ )} $
We know $ \cos 90^\circ = 1 $ so, $ \left| {\overrightarrow {\Delta v} } \right| = \sqrt {(900 + 1600 - 2(30)(40)(0))} $
 $ \Rightarrow \left| {\overrightarrow {\Delta v} } \right| = \sqrt {(2500)} = 50 $
The resultant velocity will be $ \left| {\overrightarrow {\Delta v} } \right| = 50m/s $ . Now using $ a = \dfrac{{\left| {\overrightarrow {\Delta v} } \right|}}{{\Delta t}} $ we could find the value of $ a $ to be $ \Rightarrow a = \dfrac{{50}}{{0.01}} = 5000m/{s^2} $ (since $ \Delta t = 0.01s $ )
Thus, the average acceleration of the ball during the square cut is $ 50 \times {10^2}m/{s^2} $ .

Note:
We can consider the velocity to be scalar in cases where the body does not show a change in direction or does not experience the deflection from its original path. In other situations, we are supposed to consider the velocity as a vector to obtain the exact answer by finding the resultant of the vectors involved.