Question

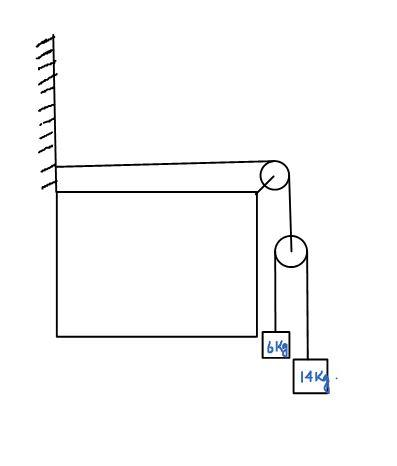
In a sonometer wire, the tension is maintained by suspending a $20kg$ mass form the free end of the wire. The fundamental frequency of vibration is $300Hz$. If the tension is provided by two masses of 6kg and 14kg suspended from a pulley as shown in the figure, the fundamental frequency will :
A. still remains $300Hz$.
B. becomes larger.
C. becomes smaller.
D. decrease in the present situation and increase if the suspended masses of 6kg and 14kg are interchanged.

Answer 1

Hint: The relationship between frequency and tension is given by, $v = k\sqrt T $ where $v$ is the frequency, $k$ is constant and $T$ is tension in the string.

Step by step solution:
Step 1.
When a mass of $20kg$ is simply connected to the pulley, the fundamental frequency is $300Hz$,the tension equals the weight.
Therefore,
$
  T = 20 \times g \\
  T = 20 \times 9.8 \\
  T = 196N \\
 $
And the relationship between frequency and tension is $v = k\sqrt T $, also it is given $v = 300Hz$.
So, let us calculate the value of k,
$
  v = k\sqrt T \\
  300 = k\sqrt {196} \\
  k = \dfrac{{300}}{{\sqrt {196} }} \\
  k = \dfrac{{300}}{{14}} \\
  k = 21.43 \\
 $………eq.(1)
Step 2.
Now let us calculate the frequency when two masses of $14kg$ and $6kg$are connected to the pulley.
Step 4.
First we'll make free body diagram,

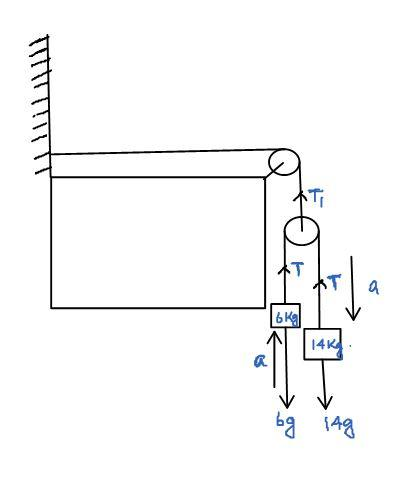
Here, the body of mass $6kg$ will move in upwards direction with $a$ acceleration and the body of mass $14kg$ will move downwards with an acceleration$a$, as acceleration in the same string will be the same. The acceleration due to gravity will act downward on both the masses and therefore, $mg$ force will act on the two masses downward and the tension will act in the upwards direction as tension always acts away from the body.
Step 5.
Let us make equations for the two bodies,
For motion of body of mass$14kg$,
$
  Mg - T = Ma \\
  14g - T = 14a \\
 $………eq.(2)
For motion of body of mass$6kg$,
$
  T - mg = ma \\
  T - 6g = 6a \\
  T = 6g + 6a \\
 $………eq.(3)
Put the value of $T$ from equation (3) in equation (2).
$14g - T = 14a$
Replace,$T = 6g + 6a$,
$
  14g - T = 14a \\
  14g - \left( {6g + 6a} \right) = 14a \\
  14g - 6g - 6a = 14a \\
  8g = 14a + 6a \\
  8g = 20a \\
  a = \dfrac{{8 \cdot \left( {9.8} \right)}}{{20}} \\
  a = 3.92m{s^{ - 2}} \\
 $
Replace the value of acceleration in equation (3).
$
  T = 6g + 6a \\
  T = 6 \cdot \left( {9.8} \right) + 6 \cdot \left( {3.92} \right) \\
  T = 82.32N \\
 $.........eq.(4)
Calculate the value of the fundamental quantity using equation$v = k\sqrt T $, we have tension $T = 82.32N$ from equation (4) and $k = 21.43$ from equation (1).
$
  v = k\sqrt T \\
  v = 21.43 \times \sqrt {82.32} \\
  v = 194.44Hz \\
 $
So, here we can see that the fundamental frequency for the new arrangement is $v = 194.44Hz$ and in the old arrangement it was $v = 300Hz$, hence the frequency has become smaller, which implies that
option C is correct.

Note: Students should observe that in the relation $v = k\sqrt T $, here $v$ is fundamental frequency and $T$ is temperature and $k$ is constant, so the value of $k$ will not change even if the condition changes, therefore we have used the value of $k$ from one condition into another.