Question

In a sonometer experiment, the string of length ‘L’ under tension vibrates in a second overtone between two bridges. The amplitude of vibration is maximum at
A.)$\dfrac{L}{6}$, $\dfrac{L}{2}$, $\dfrac{5L}{6}$
B.)$\dfrac{L}{8}$, $\dfrac{L}{4}$, $\dfrac{L}{2}$
C.)$\dfrac{L}{2}$, $\dfrac{L}{4}$, $\dfrac{L}{6}$
D.)$\dfrac{L}{6}$, $\dfrac{L}{2}$, $\dfrac{L}{6}$

Answer 1

Hint: We will first find the number and position of nodes and antinodes in terms of wavelength in the second overtone. Then we will find the wavelength of the string in terms of the length of wire. Then, by replacing the wavelength with its equivalent length of the wire, we can find the positions of the maxima.

Complete step by step solution:
The length of the given string is L and it vibrates in second overtone, that means $n=3$, that means, it will have two nodes and three antinodes and it can be represented as,

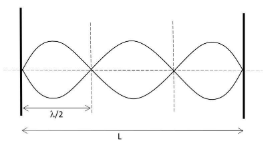
So, we can see that there are three maxima.

Suppose, the wavelength of the string be $\lambda$, and thus, length of the string in terms of wavelength can be given by $L=\dfrac{n\lambda}{2}$ and the value of n here is 3,
So, $L=\dfrac{3\lambda}{2}\implies \lambda=\dfrac{2L}{3}$

From, the figure above we can notice that the first maximum is appearing at wavelength, $\dfrac{\lambda}{4}=\dfrac{1}{4}\times \dfrac{2L}{3}=\dfrac{L}{6}$

Similarly, second amplitude maxima will be at $\dfrac{\lambda}{4}+\dfrac{\lambda}{2}=\dfrac{3\lambda}{4}$ i.e. $\dfrac{3}{4} \times \dfrac{2L}{3}=\dfrac{L}{2}$

And, third amplitude maxima will be at $\dfrac{3\lambda}{4}+\dfrac{\lambda}{2}=\dfrac{5\lambda}{4}$ i.e. $\dfrac{5}{4} \times \dfrac{2L}{3}=\dfrac{5L}{6}$

Hence, option a is the correct answer.

Additional information:
To measure the density of vibrations or tension in a string, a diagnostic instrument, sonometer is used. In medical science, they are used to test the hearing and bone density of a person.

Note: The number of maxima is denoted by the order of the overtone, in the fundamental tone, the number of maxima is one and successively increases with the increase in the order of overtones. So, in the second overtone, the number of maxima or the antinodes is three.