Question

In a series circuit, $R=300\Omega, $$L=0.9H,$$C=2.0\mu F$ and $\omega =1000rad/s$. The impedance of the circuit is
A. $1300\Omega $
B. $900\Omega $
C. $500\Omega $
D. $400\Omega $

Answer 1

Hint: The components such as resistor, inductor and capacitor are connected in series which represents an LCR circuit. Impedance is the total opposition to the flow of current offered by the components. This impedance depends on the resistor, inductive reactance and capacitive reactance. This will help you in solving this question.

Complete answer:

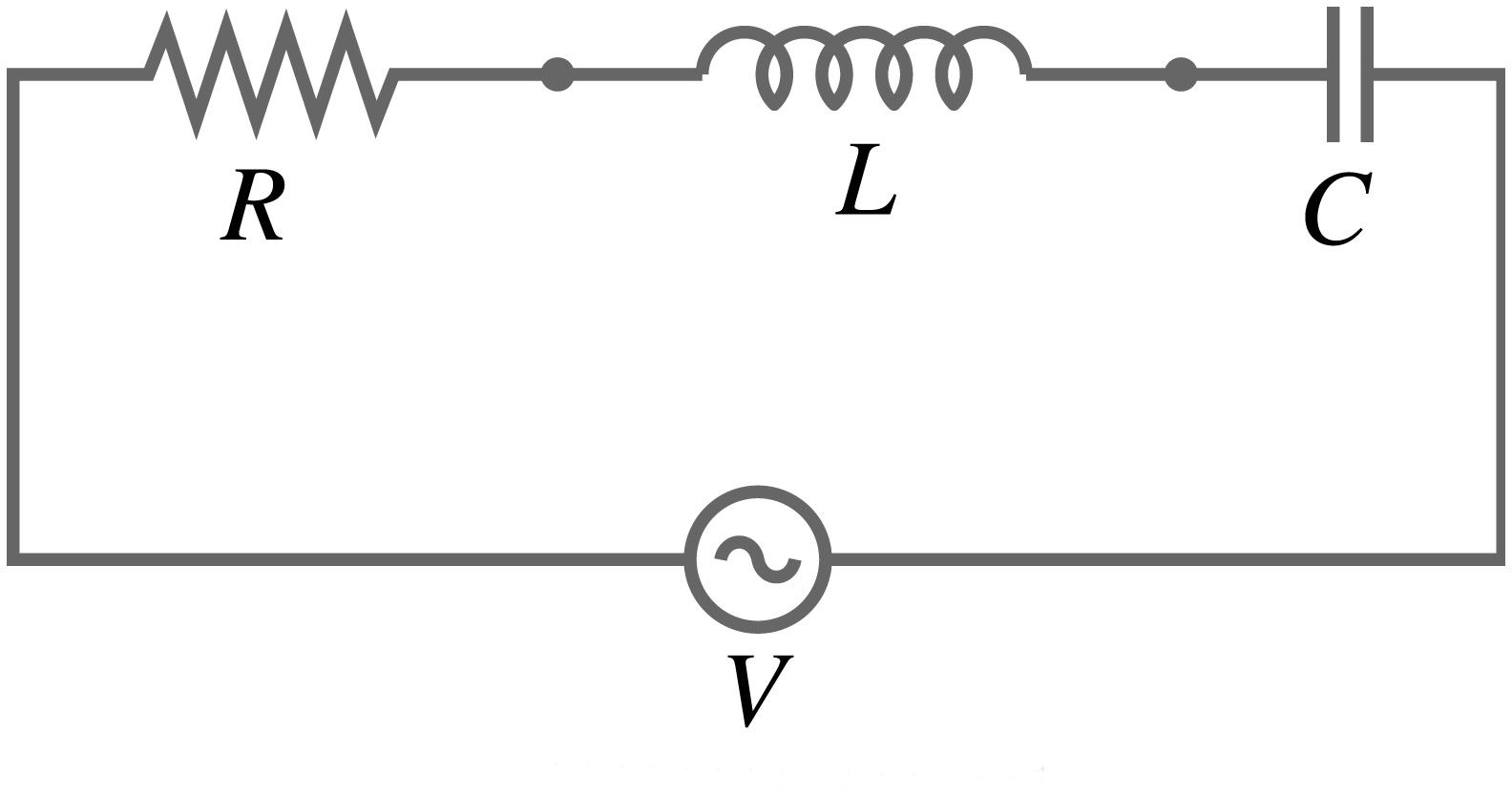
In a series LCR circuit, there are mainly three components connected, the resistor, inductor and the capacitor. Impedance is the total opposition to the flow of current offered by the components.
The impedance is given as,
$Z=\sqrt{{{R}^{2}}+{{X}^{2}}}.......(i)$
Here, Z is the impedance, R is the resistance and X is the total circuit reactance.
The total circuit reactance(X) is given as,
$X={{X}_{L}}-{{X}_{C}}$ OR \[X={{X}_{C}}-{{X}_{L}}.............(ii)\]
Where ${{X}_{L}}$and ${{X}_{C}}$ are the inductive and capacitive reactance.
The inductive reactance is found by taking the product of the angular frequency and the inductance. This can be written as,
${{X}_{L}}=\omega L$
We calculate ${{X}_{L}}$,
$\begin{align}
  & {{X}_{L}}=\omega L \\
 & {{X}_{L}}=1000rad/s\times 0.9H \\
 & {{X}_{L}}=900rad.H/s................(iii) \\
\end{align}$
The capacitive reactance is found by taking the reciprocal of the product of the angular frequency and the Capacitance. This can be written as,
${{X}_{C}}=\dfrac{1}{\omega C}$
We calculate${{X}_{C}}$,
$\begin{align}
  & {{X}_{C}}=\dfrac{1}{\omega C} \\
 & {{X}_{C}}=\dfrac{1}{1000rad/s\times 2.0\mu F} \\
 & {{X}_{C}}=500s/rad.F...............(iv) \\
\end{align}$
From (iii) and (iv), it seems that ${{X}_{L}}$is greater than ${{X}_{C}}$ .
Thus, from equation (i) and (ii), we can write that,
\[\begin{align}
  & Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}} \\
 & \Rightarrow Z=\sqrt{{{300}^{2}}+{{(900-500)}^{2}}} \\
 & \Rightarrow Z=\sqrt{90000+160000} \\
 & \Rightarrow Z=\sqrt{2500000} \\
 & \therefore Z=500\Omega \\
\end{align}\]
The impedance of the circuit is $500\Omega $.

Therefore the correct answer is option C.

Note:
If the value of Z=R, the circuit is said to be a resonant circuit which implies that the value of inductive reactance and capacitive reactance are the same. If ${{X}_{L}}$is greater than the circuit is inductive and if ${{X}_{C}}$is greater than the circuit is capacitive.