Question

In a school, 50% of the students play cricket and 40% play football, if 10% of students play both the games, then what percent of students play neither cricket nor football?
A. 10%
B. 15%
C. 20%
D. 25%

Answer 1

Hint: Consider n(C) as percent of students who play cricket, n(F) as percent of students who play football and \[n\left( C\cap F \right)\] represent both cricket and football players. Then, find the percent of students who plays both of them using formula \[n\left( C\cup F \right)=n\left( \text{C} \right)+n\left( F \right)-n\left( C\cap F \right)\] and then subtract it from 100%.

Complete step-by-step answer:
In the question, we are given a situation of a school, where 50% of the students play cricket and 40% play football while 10% play both the games. So, from the given data, we have to say that, what percent of students play neither cricket nor football.
So, let's take cricket as C and football as F. So, according to that, we suppose n(C) represent percent of students who plays cricket while n(F) represent percent of students who plays football and \[n\left( C\cap F \right)\] represents both cricket and football players.
So, we can write it as,
\[\begin{align}
  & n\left( C \right)=50\% \\
 & n\left( F \right)=40\% \\
 & n\left( C\cap F \right)=10\% \\
\end{align}\]
So, we will find total number of students who plays at least one of the sports, let it be represented as \[n\left( C\cup F \right)\] which we will find using formula,
\[n\left( C\cup F \right)=n\left( \text{C} \right)+n\left( F \right)-n\left( C\cap F \right)\]
Hence, on substitution of the values of \[n\left( \text{C} \right),n\left( F \right)\text{ and }n\left( C\cap F \right)\] we get,
\[\begin{align}
  & n\left( C\cup F \right)=50\%+40\%-10\% \\
 & \Rightarrow n\left( C\cup F \right)=80\% \\
\end{align}\]
So, total 80% of the students play either in any of the two games.
Now, as we know that, there are a total 100% students, so, we can say remaining \[\left( 100\%-80\% \right)\Rightarrow 20\%\] students neither play any of the game.So, the correct option is C.

Note: Instead of using the formula, we can use a Venn diagram. Let's represent the cricket as C and football as F. So, one can represent it as,

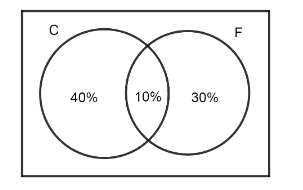
As the total box adds up to 100%, one can find the percent of students who neither play any of the sports by subtracting the total from 100%.