Question

In a right-angled triangle, the shortest sides are $5$ and$12$. Find the perimeter of the triangle.

Answer 1

Hint:The given question is related to the concept of Pythagoras theorem. Here, in this question we have to find the perimeter of the right-angled triangle. We know the fact that any side of a right-angle triangle can be found out by Pythagoras theorem if the other two sides are known. In order to solve this question, we will use the Pythagorean theorem.

Complete step by step answer:
Pythagoras theorem states that- ‘The sum of the squares of the smaller sides of a right-angled triangle is equal to the square of the greatest side/hypotenuse of the right-angled triangle’.Perimeter is the sum of all the sides present in the figure. It can be calculated after finding the length of all the sides.Given, shortest sides are $5$ and $12$.The right-angled triangle looks like-

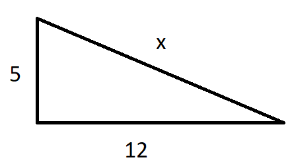
The base is $12$ units while the perpendicular is $5$ units. We will use the Pythagoras theorem to find the greatest side or the hypotenuse of the triangle. Let the hypotenuse be $x$ units. So, by Pythagoras theorem,
${\text{hypotenuse}^2} = {\text{base}^2} + {\text{perpendicular}^2}$
$\Rightarrow {x^2} = {\left( 5 \right)^2} + {\left( {12} \right)^2} \\
\Rightarrow {x^2} = 25 + 144 \\
\Rightarrow {x^2} = 169 \\ $
Now, we apply square root on both the sides of the equation and we get,
$\sqrt {{x^2}} = \sqrt {169} \\
\Rightarrow x = 13 \\ $
So, the greatest side or the hypotenuse is $13$ units.Now, we have found all the sides of the right-angled triangle. So, the perimeter is
$\text{Perimeter} = \text{Sum of all the sides}\\
\Rightarrow\text{Perimeter}= 5 + 12 + 13 \\
\therefore\text{Perimeter} = 30 \\ $
Therefore, the perimeter of the triangle is $30$ units.

Note: The given question was easy to solve because we knew about the Pythagoras theorem. Students should avoid making calculation mistakes while finding out the sides of the triangle. Making a figure, like we did in the above question helps a lot in avoiding confusion. If the measuring unit (m, cm) is not given like in this question, so we use word units.