Question

In a right-angle triangle in which \[\angle {B^o} = {90^o}\], a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that tangent to the circle at P bisects BC.

Answer 1

Hint: We’ll first perform the construction by joining the points B and P also we’ll make a tangent at point P which intersects the line BC at some point. In order to prove, we’ll try to show that that intersection point is the midpoint of the line BC. Which will imply our required proving.

Complete step-by-step answer:
We have given, ABC is a right-angle triangle, right-angled at B. A circle is drawn With AB as diameter which intersects hypotenuse at point p. We have done a construction that is a tangent to the circle at point P. Which is PQ, intersecting BC at Q. Also, we have joined the points B and P which gives us line BP.
Now Observe that, PQ and BQ are tangents to the circle from the same external point Q. And we know, If we draw 2 tangents to a circle from the same external points then lengths of the tangents will be the same. We this argument we can conclude that $ PQ = BQ - - - - - (1) $

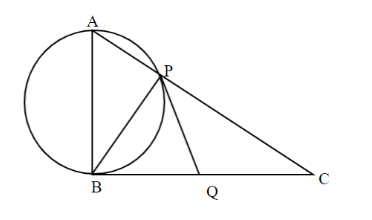
In $ \vartriangle PBQ $ , the lengths of two sides are the same on the same base that is BP so their angle will also be the same.
 $ \angle PBQ = \angle BPQ - - - - (2) $
Now, we have given that Circle is made taking AB as diameter.
 $ \angle APB = {90^o} $ (Angle on semicircle is right angled.)
And, $ \angle APB + \angle BPC = {180^o} $ (Angle on straight line is always $ {180^o} $ )
Putting the value of $ \angle APB = {90^o} $ , we get
 $
  {90^o} + \angle BPC = {180^o} \\
   \Rightarrow \angle BPC = {180^o} - {90^o} \\
   \Rightarrow \angle BPC = {90^o} \\
  $

Now, In $ \vartriangle PBC $
Sum of angles of the triangle is $ {180^o} $ . So,
 $
  \angle PBC + \angle PCB + \angle BPC = {180^o} \\
   \Rightarrow \angle PBC + \angle PCB + {90^o} = {180^o} \\
   \Rightarrow \angle PBC + \angle PCB = {180^o} - {90^o} \\
   \Rightarrow \angle PBC + \angle PCB = {90^o} - - - - - (3) \\
  $
Also observe from the figure that $ \angle BPC = \angle BPQ + \angle CPQ $
We know that $ \angle BPC = {90^o} $ Putting it’s value, we get
 $ \angle BPQ + \angle CPQ = {90^o} - - - - (4) $
From equation (3) and (4) we get,
 $ \angle PBC + \angle PCB = \angle BPQ + \angle CPQ $
But, $ \angle BPQ = \angle PBC $ (From equation (2))
Hence, $ \angle PCB = \angle CPQ $
Which can also be written as $ \angle PCQ = \angle CPQ $ because $ \angle PCB = \angle PCQ $
Now, In $ PCQ $
 $ \angle PCQ = \angle CPQ $
 $ \therefore PQ = QC - - - - (5) $
From equation (5) and (1) we can say,
 $ CQ = BQ $
Hence, Q is the midpoint of the line segment BC. Thus, tangent at P bisects the side BC.
Hence proved.

Note: This question can also be asked in the reverse direction. By reverse direction we mean, they’ll give the information that point Q is the midpoint for the line segment BC and ask us to prove that $ \angle APB $ is right-angle or AB is diameter or AB divides the circle into two equal parts. That’s the beauty of the geometry that the same sentence can be said in several ways.