Question

In a right triangle with sides x and y, hypotenuse z the attitude drawn on the hypotenuse is a then
$\begin{align}
  & \left( a \right)xy={{a}^{2}} \\
 & \left( b \right)\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{a} \\
 & \left( c \right){{x}^{2}}+{{y}^{2}}=2{{a}^{2}} \\
 & \left( d \right)\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}=\dfrac{1}{{{a}^{2}}} \\
\end{align}$

Answer 1

Hint: To solve the question given above, first we will draw a right angled triangle with base x, perpendicular y and hypotenuse z. Then we will draw a perpendicular on the hypotenuse from the opposite vertex. Now, we will find the area of this triangle in terms of x and y. After that, we will find the area in terms of a and z. Now, we will compare both areas and find the relation between x, y and a.

Complete step-by-step answer:

It is given in a question that there is a right angled triangle. We will assume that the side x is base and side y is perpendicular. Also z is the hypotenuse and a is perpendicular drawn to the hypotenuse from the opposite vertex. The right angle triangle is shown below:

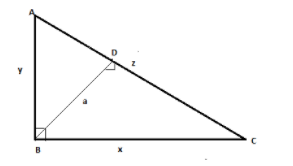
As, we can see that AC is the hypotenuse, BC is the base and AB is perpendicular. Now, we will calculate the area of triangle ABC. Let its area be A. The area of triangle with given perpendicular and base is calculated by the formula shown: $Area=\dfrac{1}{2}\times perpendicular\times base$
Now, to calculate the area of the triangle ABC, we will take AB as perpendicular and BC as base. Thus the area of triangle will become:
$\begin{align}
  & A=\dfrac{1}{2}\times \left( AB \right)\times \left( BC \right) \\
 & \Rightarrow A=\dfrac{1}{2}\times x\times y \\
 & \Rightarrow A=\dfrac{xy}{2}............\left( 1 \right) \\
\end{align}$
Now, we can see from the above figure that a is perpendicular to the hypotenuse z. So, we will take a as perpendicular and the hypotenuse AC as base. Thus, the area of triangle ABC will be:
$\begin{align}
  & A=\dfrac{1}{2}\left( BD \right)\times AC \\
 & \Rightarrow A=\dfrac{1}{2}\times a\times z \\
 & \Rightarrow A=\dfrac{az}{2}...........\left( 3 \right) \\
\end{align}$
Now, we will apply the Pythagoras theorem in \[\vartriangle ABC\]. According to Pythagoras theorem, if in a right angled triangle, H is hypotenuse , B is the base and P is the perpendicular then we have following reaction: ${{H}^{2}}={{P}^{2}}+{{B}^{2}}$
Similarly, we can say that, in\[\vartriangle ABC\]:
$\begin{align}
  & {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}} \\
 & {{z}^{2}}={{y}^{2}}+{{x}^{2}} \\
 & \Rightarrow z=\sqrt{{{y}^{2}}+{{x}^{2}}}.............\left( 4 \right) \\
\end{align}$
Now, we will substitute the value of z from (4) to (3):

$\Rightarrow A=\dfrac{a\sqrt{{{y}^{2}}+{{x}^{2}}}}{2}..........\left( 5 \right)$
On comparing (4) and (5), we will get:
$\begin{align}
  & \dfrac{xy}{2}=\dfrac{a\sqrt{{{y}^{2}}+{{x}^{2}}}}{2} \\
 & xy=a\sqrt{{{y}^{2}}+{{x}^{2}}} \\
\end{align}$
On squaring both sides, we will get:
$\begin{align}
  & {{\left( xy \right)}^{2}}={{\left( a \right)}^{2}}\left( {{y}^{2}}+{{x}^{2}} \right) \\
 & \Rightarrow {{x}^{2}}{{y}^{2}}={{a}^{2}}\left( {{x}^{2}}+{{y}^{2}} \right) \\
 & \Rightarrow \dfrac{{{x}^{2}}{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}={{a}^{2}} \\
\end{align}$
Now, we will take the inverse on both sides. Thus we have:
$\begin{align}
  & \Rightarrow \dfrac{{{x}^{2}}+{{y}^{2}}}{{{x}^{2}}{{y}^{2}}}=\dfrac{1}{{{a}^{2}}} \\
 & \Rightarrow \dfrac{{{x}^{2}}}{{{x}^{2}}{{y}^{2}}}+\dfrac{{{y}^{2}}}{{{x}^{2}}{{y}^{2}}}=\dfrac{1}{{{a}^{2}}} \\
 & \Rightarrow \dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{x}^{2}}}=\dfrac{1}{{{a}^{2}}} \\
\end{align}$
Hence, option (d) is correct.

Note: The above question can also be solved alternatively by the following method:

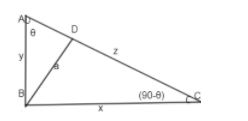
From \[\vartriangle ABC\], we have:
$\begin{align}
  & \sin \theta =\dfrac{BD}{AD} \\
 & \Rightarrow \sin \theta =\dfrac{a}{y}...........\left( 1 \right) \\
\end{align}$
From \[\vartriangle BCD\], we have:
$\begin{align}
  & \sin \left( 90-\theta \right)=\dfrac{BD}{BC} \\
 & \Rightarrow \cos \theta =\dfrac{a}{x}..........\left( 2 \right) \\
\end{align}$
We will square (1) and (2) and add. Thus we will get:
${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =\dfrac{{{a}^{2}}}{{{y}^{2}}}+\dfrac{{{a}^{2}}}{{{y}^{2}}}\Rightarrow 1=\dfrac{{{a}^{2}}}{{{y}^{2}}}+\dfrac{{{a}^{2}}}{{{y}^{2}}}\Rightarrow \dfrac{1}{{{a}^{2}}}=\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{x}^{2}}}$.