Question

In a right angled triangle, the other two angles are:
A. Acute
B. Obtuse
C. Right
D. None of these

Answer 1

Hint: In this question, we are given a right angled triangle and we need to find two other angles. For this, we will first understand the meaning of acute, obtuse and right angles. Then, we will draw a diagram to understand more clearly. Then we will use angle sum property to conclude our answer. Angle sum property states that the sum of the angles of the triangle is equal to ${{180}^{\circ }}$.

Complete step-by-step answer:
Here, we are given a right angled triangle and we have to tell nature about two other angles. Let us first understand the meaning of acute, obtuse and right angles.
Acute angle- An angle which is less than ${{90}^{\circ }}$ is called an acute angle.
Obtuse angle- An angle which is more than ${{90}^{\circ }}$ is called an obtuse angle.
Right angle- An angle which is exactly equal to ${{90}^{\circ }}$ is called a right angle.
Now let us draw a diagram:

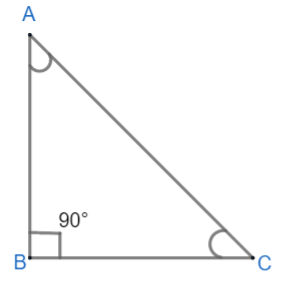
Here we have considered $\angle B$ as ${{90}^{\circ }}$. Hence, we need to find the nature of other two angles.
We know that, angle sum property of the triangle states that the sum of the angles of a triangle is equal to ${{180}^{\circ }}$.
So in triangle ABC we have:
\[\angle A+\angle B+\angle C={{180}^{\circ }}\]
Putting value of $\angle B$ as ${{90}^{\circ }}$ we get:
\[\begin{align}
  & \Rightarrow \angle A+{{90}^{\circ }}+\angle C={{180}^{\circ }} \\
 & \Rightarrow \angle A+\angle C={{180}^{\circ }}-{{90}^{\circ }} \\
 & \Rightarrow \angle A+\angle C={{90}^{\circ }} \\
\end{align}\]
Now, as we know, any angle cannot be ${{0}^{\circ }}$ so any of the angle A or angle C cannot be equal to ${{90}^{\circ }}$ and hence, cannot be right angles.
Also, none of the angles can be greater than ${{90}^{\circ }}$ otherwise others will be negative which is not possible. So angle cannot be obtuse angle.
So we conclude that, for the sum of both angles to be equal to ${{90}^{\circ }}$ we need both angles less than ${{90}^{\circ }}$. Hence, we need an acute angle.
So, acute is the correct answer.
Hence, option A is the correct answer.

So, the correct answer is “Option A”.

Note: For solving this question, students must know the definition of acute, obtuse and right angles. We can also see from the diagram that angle A and angle C are smaller than ${{90}^{\circ }}$ and hence, acute angles. If in a triangle, one of the angles is obtuse, then also the other two angles are acute angles.