Question

In a rhombus ABCD ,prove that \[4A{B^2} = A{C^2} + B{D^2}\]

Answer 1

Hint: In a rhombus, all the four sides are equal and diagonal intersect each other at right angle and so apply the Pythagoras theorem in all four formed triangles as \[A{C^2} = A{B^2} + B{C^2}\] and sum up the area of all the four triangles and substitute using the conditions and hence using the above concept of rhombus. We can prove as per the given data.

Complete step-by-step answer:
 As given to prove that \[4A{B^2} = A{C^2} + B{D^2}\] .
Diagram:

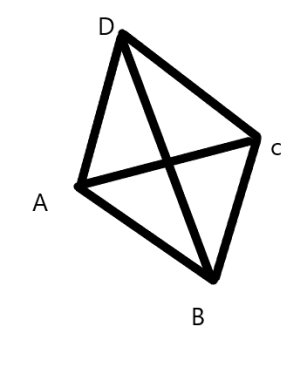
Let O be the point of intersection of diagonals
Hence, from the properties of Rhombus as \[AB = BC = CD = DA\]
And all the angles are at right angle and so we can apply Pythagoras theorem in \[\Delta AOB,\Delta AOD,\Delta COD,\Delta BOC\]
And so applying Pythagoras theorem in the first triangle \[\Delta AOB\] as
 \[ \Rightarrow \] \[A{O^2} + O{B^2} = A{B^2}\]
Now applying Pythagoras theorem in another triangle as \[\Delta BOC\]
\[ \Rightarrow \] \[B{O^2} + O{C^2} = B{C^2}\]
And apply the theorem in third triangle also as \[\Delta DOC\] ,
\[ \Rightarrow \] \[D{O^2} + O{C^2} = D{C^2}\]
And again applying in \[\Delta AOD\]
So, it can be applied as \[A{D^2} = A{O^2} + O{D^2}\] .
Hence, as per the properties of Rhombus as the diagonals of rhombus is also equal and so AC=BD.
And also we know
 \[AO = OC = \dfrac{{AC}}{2}\]
Applying same on another side as
 \[BO = OD = \dfrac{{BD}}{2}\]
Hence, adding all the above four equation in which Pythagoras theorem is applied and so
\[ \Rightarrow \] \[A{O^2} + O{B^2} + O{C^2} + B{O^2} + D{O^2} + O{C^2} + A{O^2} + O{D^2} = A{B^2} + B{C^2} + C{D^2} + D{A^2}\]
As all sides are equal AB=BC=CD=DA and so,
\[ \Rightarrow \] \[A{O^2} + O{B^2} + O{C^2} + B{O^2} + D{O^2} + O{C^2} + A{O^2} + O{D^2} = 4A{B^2}\]
Also, we know that
 \[AO = OC = \dfrac{{AC}}{2}\] and \[BO = OD = \dfrac{{BD}}{2}\]
\[ \Rightarrow \] \[2(A{O^2} + O{C^2}) + 2(B{O^2} + D{O^2}) = 4A{B^2}\]
So, \[4A{O^2} + 4B{O^2} = 4A{B^2}\]
It can also be simplified as
\[ \Rightarrow \] \[{(2AO)^2} + {(2BO)^2} = 4A{B^2}\]
Hence, substituting all the above values in the given condition as
\[ \Rightarrow \] \[{(AC)^2} + {(BD)^2} = 4A{B^2}\]
Hence proved.
Note: You should always make a diagram first for better understanding, also remember to name the vertices and don’t mix up the names of the edges, this can lead to incorrect answers.
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length.
It follows that any rhombus has the following properties:
Opposite angles of a rhombus have equal measure.
The two diagonals of a rhombus are perpendicular; that is, A rhombus is an Orthodiagonal quadrilateral. Its diagonals bisect opposite angles.