Question

In a rhombus ABCD, AC = 10 cm and BD = 24 cm, then find the perimeter of rhombus ABCD.

Answer 1

Hint: We will first draw the rhombus and then using the lengths of the diagonals, we will find the length of the side of the rhombus using the Pythagorean Theorem and then multiply that with 4 to get the perimeter.

Complete step-by-step answer:
Let us first draw it to understand it better.

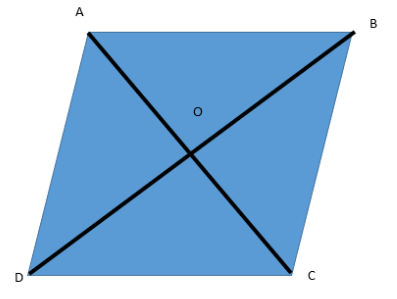
Here, AC = 10 cm and BD = 24 cm.
We know that the diagonals of a rhombus bisect each other at right angles.
Hence, the triangles AOB, BOC, COD and DOA are all right angled triangles.
Since at O, the diagonals are bisected. Hence, AO = OC and DO = OB.
Using these and lengths of the diagonals, we get: AO = OC = 5 cm and DO = OB = 12 cm.
Since the Pythagorean Theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“.
Since, AOB is a right angled triangle which is right angled at O. Using the Pythagorean Theorem, we will get:
$ \Rightarrow A{B^2} = A{O^2} + O{B^2}$
Putting in the values, we get:-
$ \Rightarrow A{B^2} = {5^2} + {12^2} = 169$
$ \Rightarrow AB = 13$
Hence, the side of rhombus is 13 units.
Since, the perimeter of a rhombus is given by $P = 4 \times Side$.

Hence, $P = 4 \times 13 = 52$ square units.

Note: The students might wonder that the perimeter of the square and rhombus is the same. What is the reason behind that? Let us understand that. We know that both squares and rhombus have 4 sides. Now since all sides are equal length in both, therefore instead of adding them individually, we just multiply 1 side with 4.
The students must not make the mistake of applying the Pythagorean Theorem directly on both the diagonals however because we always need a right angled triangle to do so. So, you first need to justify the reason for using the theorem.