Question

In a regular hexagon $ABCDEF$, $AB||ED||$the x- axis. What is the slope of the sides?

Answer 1

Hint: First, draw the figure as per given conditions. Then use the fact that the slope of sides parallel to x- axis is 0 and the slope of other sides can be found by the angles they form with positive x-axis because $Slope = \tan \theta $.

Complete step-by-step answer:
Let us first draw the figure as shown below:
     

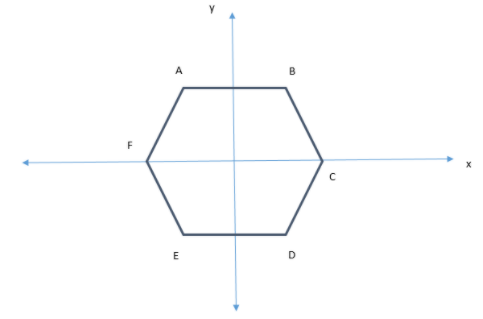
We see that $AB||ED||$ the x- axis in above figure as given.
Now, since the hexagon is regular. So, all sides are of equal length.
Regular polygon means polygon has all the sides of equal lengths and all equal angles.
So, AB = BC = CD = DE = EF = AF …….(1)
And $\angle A = \angle B = \angle C = \angle D = \angle E = \angle F$ …..(2)
We also know that the sum of all angles of a polygon is $(n - 2) \times {180^ \circ }$.
So, sum of all angles in hexagon will be $(6 - 2) \times {180^ \circ } = {720^ \circ }$
Using (2) and (3), we get:
$\angle A + \angle B + \angle C + \angle D + \angle E + \angle F = {720^ \circ }$
Hence, $\angle A = \angle B = \angle C = \angle D = \angle E = \angle F = {120^ \circ }$……(3)
Now, let us join AD, BE and FC as shown below with the center named as O:
     

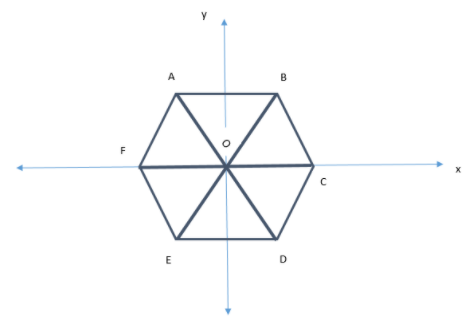
Since the angle around a point is always \[\;{360^ \circ }\].
So, $\angle AOB + \angle BOC + \angle COD + \angle DOE + \angle EOF + \angle FOA = {360^ \circ }$ …..(4)
Consider $\vartriangle AOB$ and $\vartriangle DOE$:
$AB = DE$ (Sides of regular polygon)
$\angle AOB = \angle DOE$ (Vertically opposite angles)
$\angle OAB = \angle ODE$ (Alternate angles)
Hence, $\vartriangle AOB \cong \vartriangle DOE$ (ASA property)
ASA property states that if two triangles have two pairs or corresponding equal angles and one pair of corresponding equal sides, then both the triangles are congruent.
Hence, $AO = DO$ and $OB = OE$ (By C.P.C.T.)
CPCT stands for Corresponding parts of congruent triangles. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.
Similarly, we can do for all the triangles and hence get:
$AO = BO = CO = DO = EO = FO$
Hence, $\angle OAB = \angle OBA$, $\angle OBC = \angle OCB$, $\angle OCD = \angle ODC$, $\angle ODE = \angle OED$ and
$\angle OFA = \angle OAF$.
Using (3) here, We have:
$\angle OAB = \angle OBA = \angle OBC = \angle OCB = \angle OCD = \angle ODC = \angle ODE = \angle OED = \angle OFE = \angle OEF = \angle OFA = \angle OAF$
And all the angles are ${60^ \circ }$.
Now, we are given that $AB||ED||$the x- axis.
Hence, Slope of AB and ED is 0.
Because the angle between these lines and x- axis is ${0^ \circ }$ and slope = $\tan \theta $, where $\theta $ is the angle
between the line and positive x axis and $\tan {0^ \circ } = 0$.
Slope of BC = Slope of OD = Slope of EF ($BC||OD||EF$)
Parallel lines have the same slopes.
Slope of OD will be $\tan {120^ \circ }$. (It makes angle of ${120^ \circ }$ with positive x axis)
$\tan {120^ \circ } = \tan {(90 + 30)^ \circ } = - \cot {30^ \circ } = - \sqrt 3 $
Because $\tan ({90^ \circ } + \theta ) = - \cot \theta $
Hence, Slope of BC = Slope of OD = Slope of EF = $ - \sqrt 3 $.
Slope of CD = Slope of BO = Slope of FA ($BO||CD||FA$)
Slope of OD will be $\tan {60^ \circ }$. (It makes angle of ${60^ \circ }$ with positive x axis)
And $\tan {60^ \circ } = \sqrt 3 $.
Hence, Slope of CD = Slope of BO = Slope of FA = $\sqrt 3 $.
Thus, we have found all the slopes.

Note: The students might make the mistake of measuring the angle of lines from the nearest part of
axis, but we need to keep in our mind, the fact that, we need to measure them from positive x axis in
anti-clockwise direction always.