Question

In a rectangle $ABCD$, point $X$ and $Y$ are the midpoints of \[AD\] and \[DC\], respectively. Lines $BX$ and $CD$ when extended intersect at $E$, lines $BY$ and $AD$ when extended intersect at \[F\]. If the area of $ABCD$ is 60 then the area of $BEF$ is
A. 60
B. 80
C. 90
D. 120

Answer 1

Hint: First of all, draw the diagram corresponding to the given condition. Prove that $\vartriangle XED$ and $\vartriangle XBA$ are congruent and $\vartriangle DFY$ and $\vartriangle CBY$ are congruent. Then, express \[\vartriangle BEF = \square BXDY + \vartriangle DFY + \vartriangle XED + \vartriangle DEF\], substitute the congruent values to form a rectangle $ABCD$. Substitute the given area and compute the area of $BEF$.

Complete step-by-step answer:
We will begin by drawing the diagram of the given condition, which states that there is a rectangle $ABCD$ , where point $X$ and $Y$ are the midpoints of \[AD\] and \[DC\]. Extend the lines $BX$ and $CD$ when extended intersect at $E$. Similarly, extend lines $BY$ and $AD$ when extended intersect at \[F\].

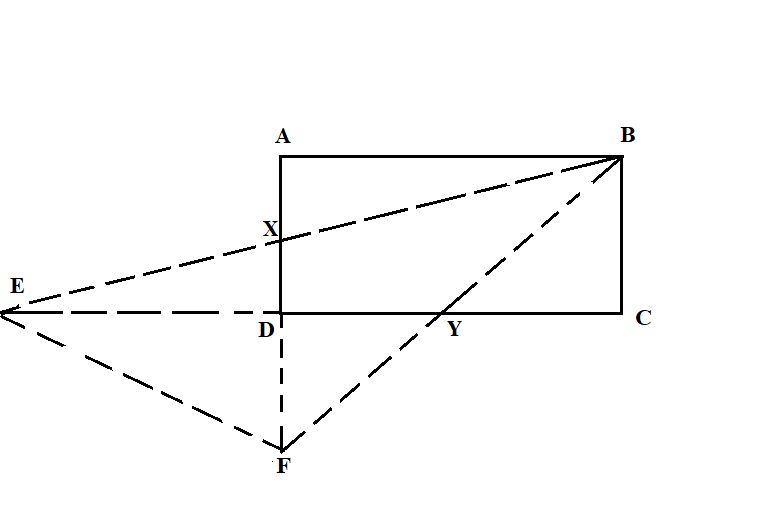
Let the length of the side $AB$ be $a$ and let the length of side $BC$ be $b$.
Then, we know that the area of rectangle is the product of its sides.
Hence, area of rectangle $ABCD$ is $ab$ which is also given equal to 60
That is, $ab = 60$
Next, we will consider triangles $\vartriangle XED$ and $\vartriangle XBA$
Here, $AX = XD$ as $X$ is the mid-point of $AD$.
Next, $\angle XDE = \angle BAX$ as they are right angles.
Also, $\angle BXA = \angle EXD$ as they are vertically opposite angles.
Therefore, $\vartriangle XED \cong \vartriangle XBA$ by ASA (angle-side-angle criterion)
We will now consider $\vartriangle DFY$ and $\vartriangle CBY$
Here, $DY = YC$ as $Y$ is the mid-point of $CD$.
Next, $\angle YDF = \angle BCY$ as they are right angles.
Also, $\angle BYC = \angle FYD$ as they are vertically opposite angles.
Therefore, $\vartriangle DFY \cong \vartriangle CBY$ by ASA (angle-side-angle criterion)
Also, \[\vartriangle BEF = \square BXDY + \vartriangle DFY + \vartriangle XED + \vartriangle DEF\]
Which is also equal to
$
  \vartriangle BEF = \square BXDY + \vartriangle CBY + \vartriangle XBA + \vartriangle DEF \\
   \Rightarrow \vartriangle BEF = \square ABCD + \vartriangle DEF \\
$
We are given that If the area of $ABCD$ is 60
Therefore, \[\vartriangle BEF = 60 + \vartriangle DEF\]
Moreover, the area of \[\vartriangle DEF\] will be \[\dfrac{1}{2}ab\] as $a$ is the height of the triangle and $b$ is the base of the triangle as the area of triangle is half the product of the base and height.
Here, $ab$ is the area of the rectangle $ABCD$, which is equal to 60 square units.
Then, \[\dfrac{1}{2}ab = \dfrac{1}{2}\left( {60} \right) = 30\]
Now,
$
  \vartriangle BEF = 60 + \vartriangle DEF \\
   \Rightarrow \vartriangle BEF = 60 + 30 \\
  \vartriangle BEF = 90 \\
$
Thus the area of \[\vartriangle BEF\] is 90 square units.
Hence, option C is correct.
Note: One must know different rules of congruence to prove two triangles congruent. Congruent triangles have the same length of sides , same angles and same area. The diagram should be made correctly to avoid mistakes. Also, each angle of the rectangle is a right angle.