Question

In a quadrilateral the sides are ${\text{9, 40, 28, 15}}$units and the angle between the first two sides is a right angle. The area of quadrilateral is
a) $106$ sq. units
b) $206$sq. units
c) $306$ sq. units
d) $406$sq. units

Answer 1

Hint: In this question we have to find the value of the area of the quadrilateral. For that we are going to solve using Pythagoras theorem. And also we are going to calculate using quadrilateral and have given a complete step-by-step solution.

Formula used: Pythagoras theorem formula,
Consider the triangle is given,
Where “a” is the perpendicular side,
“b” is the base,
“c” is the hypotenuse side.
${{\text{c}}^{\text{2}}}{\text{ = }}{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}$
Pythagoras theorem statement: “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the two sides”.

Complete step-by-step solution:

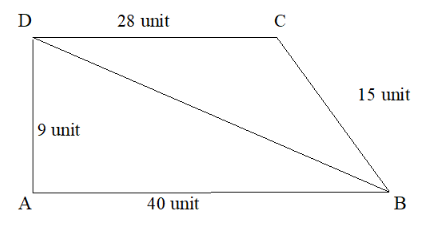
From the given, $\angle {\text{DAB}}$ is a right angle triangle.
Using Pythagoras theorem,
\[\therefore {\text{D}}{{\text{B}}^{\text{2}}}{\text{ = D}}{{\text{A}}^{\text{2}}}{\text{ + A}}{{\text{B}}^{\text{2}}}\]
Substituting the values in given,
$ \Rightarrow {\text{D}}{{\text{B}}^{\text{2}}}{\text{ = }}{{\text{9}}^{\text{2}}}{\text{ + 4}}{{\text{0}}^{\text{2}}}$
Taking square root on both sides we get,
$ \Rightarrow {\text{DB}} = \sqrt {81 + 1600} $
Hence,
${\text{DB = 41}}$unit
Let us consider the $\vartriangle {\text{DAB}}$,
We have ${\text{s}} = \dfrac{{9 + 40 + 41}}{2}$
$ \Rightarrow {\text{s}} = \dfrac{{90}}{2}$
Hence,
${\text{s}} = 45$unit
Since, area of $\vartriangle {\text{DAB = }}{{\text{A}}_1} = \sqrt {{\text{s (s - a) (s - b) (s - c)}}} $
Let substitute the values,
$ \Rightarrow \sqrt {45(45 - 9)(45 - 40)(45 - 41)} $
Simplifying we get,
$ \Rightarrow \sqrt {45 \times 36 \times 5 \times 4} $
Thus,
$ \Rightarrow 180$sq. unit
Let us consider the $\vartriangle {\text{DCB}}$,
We have ${\text{s}} = \dfrac{{28 + 15 + 41}}{2}$
$ \Rightarrow {\text{s}} = \dfrac{{84}}{2}$
Hence,
$ \Rightarrow {\text{s}} = 42$unit
Area of $\vartriangle {\text{DCB = }}{{\text{A}}_2} = \sqrt {{\text{s (s - a) (s - b) (s - c)}}} $
$ \Rightarrow \sqrt {42 \times \left( {42 - 38} \right) \times \left( {42 - 15} \right) \times \left( {42 - 41} \right)} $sq. units
Simplifying we get,
$ \Rightarrow \sqrt {42 \times 14 \times 27 \times 1} $
Thus,
$ \Rightarrow 126$sq. units
Hence, area of quadrilateral $ = {{\text{A}}_{\text{1}}}{\text{ + }}{{\text{A}}_{\text{2}}}$
$ \Rightarrow \left( {180 + 126} \right)$

Hence, area of quadrilateral $ = 306$sq. units

Note: We already know that, in geometry, a quadrilateral can be defined as a closed, two-dimensional shape which has four straight sides. The polygon has four vertices or corners. We can find the shape of quadrilaterals in various things around us, like a chess board, a deck of cars, a kite, and a tub of popcorn, a sign board and in an arrow.