Question

In a quadrilateral ABCD, AB = AD and CB = CD; but the sides are not all equal. Which of the diagonals (if either) is an axis of symmetry?

Answer 1

Hint: We use any general image figure to understand the concept. We try to draw diagonals to find out if the diagonal divides the figure into two equal figures. Also, we try to find the equal sides which proves the symmetry.

Complete step-by-step solution:
AB, BC, and CD, DA represent two pairs of equal adjacent sides. We know that in a kite, the four sides can be grouped into two pairs of equal-length sides that are adjacent.
Hence, the given quadrilateral is a kite form.
Now, as the adjacent sides are equal, only one diagonal will be able to divide the figure into two equal parts. So, anyone of the diagonals will be the axis of symmetry.

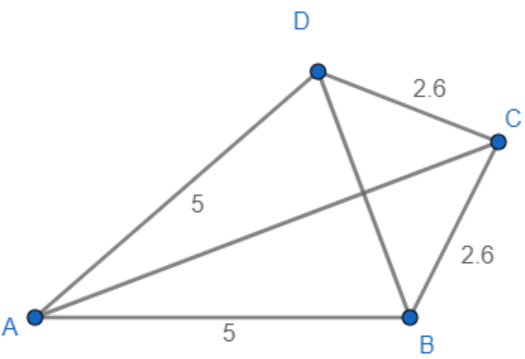
In the figure, we can see that the diagonal AC divides the figure into two triangles where AB = AD and CB = CD. AB and BC are in one triangle, whereas AD and CD are in another triangle.
So, the quadrilateral is symmetric with respect to the diagonal AC.
But, in the figure, we can also see that the diagonal BD doesn’t divide the figure into two symmetrical triangles where $AB\ne BC$ and $AD\ne CD$. AB and AD are in one triangle, whereas BC and CD are in another triangle.
So, the quadrilateral is symmetric with respect to the diagonal AC.

Note: Although we could exactly mention which diagonal is the axis of symmetry and which one is not. It was only possible because of the given of the equality of the sides. If that was not given, we only could have mentioned that one diagonal will be the axis of symmetry, and the other one not. We could not have been sure about its name of the diagonal.