Question

In a perpendicular bisector of a line segment PQ, the triangle APQ and BPQ are:

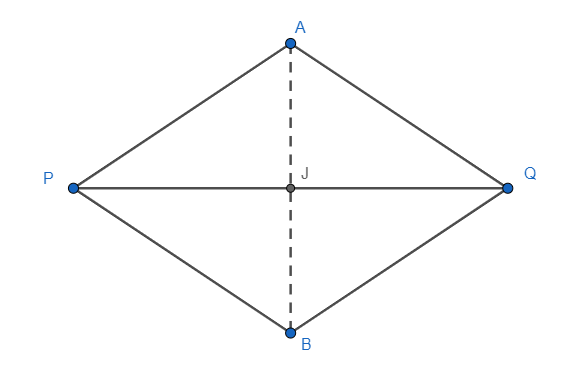
(a) Acute
(b) Obtuse
(c) Scalene
(d) Isosceles

Answer 1

Hint: First start with $\Delta APQ$ and as we know AJ is the perpendicular bisector of the line PQ. Now try to prove that $\Delta AJP\text{ and }\Delta \text{AJQ}$ congruent and draw the required result. The result you get for $\Delta APQ$ will also be valid for $\Delta BPQ$ , as they have all their properties the same and mirror images of each other.

Complete step by step solution:
Let us start the solution to the above question by focusing on the triangle $APQ$ , with the perpendicular bisector of the side PQ passing through A and bisecting PQ at J. Let us draw a representative diagram of the considered situation for better understanding.

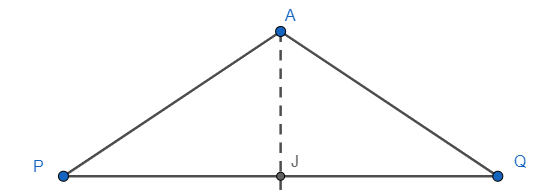
Now, if we see in $\Delta AJP\text{ and }\Delta \text{AJQ}$ , we will find that
AJ is common. As AJ is the perpendicular bisector of PQ, we can say PJ=QJ and $\angle AJP=\angle AJQ$ , as both are equal to $90{}^\circ $ .
So, using the RHS criteria we can say that $\Delta AJP\text{ }\cong \Delta \text{AJQ}$ . As the two triangles are congruent, the corresponding sides of the triangles are equal according to the rule of CPCT (corresponding sides of congruent triangles). Therefore, we can say that AP=AQ.
As AQ=AP, we can say $\Delta APQ$ is an isosceles triangle, because isosceles triangles are those triangles which have two of its sides equal.
Similarly, as $\Delta AJP\text{ and }\Delta \text{AJQ}$ are similar in all aspects and have the same properties we can say that both are isosceles triangles.
Therefore, the answer to the above question is option (d).

Note: We have not reported the answer as acute or obtuse because the triangle can be either acute or obtuse, there is no constraint on the value of the angles, the one constraint on relation between the angles is that the angles opposite to equal sides of the isosceles triangle are equal. So, there is no compulsory restriction that the triangle should be acute or obtuse, so we cannot consider option (a) or (b) to be correct. If you want you can learn the result that If one of the perpendicular bisectors of a triangle passes through its opposite vertex, then the triangle is an isosceles triangle.