Question

In a parallelogram the value of \[\angle A-\angle C\] .
(A) \[{{90}^{0}}\]
(B) \[{{100}^{0}}\]
(C) \[{{0}^{0}}\]
(D) \[{{180}^{0}}\].

Answer 1

Hint: In a parallelogram ABCD, we have AB parallel to CD and the diagonal AC as a transversal. Alternate angles are equal which means \[\angle DCA\] and \[\angle CAB\] are equal. Similarly, we have \[\angle DAC\] and \[\angle BCA\] equal to each other where AD is parallel to BC and AC is a transversal.

Complete step-by-step solution -

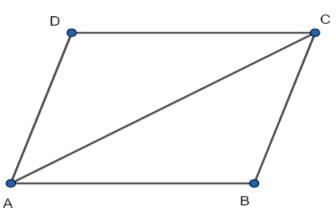
In the given figure, we have a parallelogram ABCD.
In a parallelogram, we have opposite sides parallel to each other. It means that AB is parallel to CD. Since the sides, BC and AD are also opposite to each other. So, BC is also parallel to AD.
We have to find the subtraction of \[\angle A\] and \[\angle C\].
 AB and CD are opposite sides and parallel to each other.
Here, the diagonal AC is a transversal.
\[\angle ACD\] and \[\angle CAB\] are alternate angles and for two parallel lines, alternate angles are equal to each other. It means \[\angle ACD\] and \[\angle CAB\] are equal to each other.
\[\angle ACD=\angle CAB\] ………………….(1)
Also, the side AD is parallel to BC and also the diagonal AC is a transversal here.
\[\angle ACB\] and \[\angle CAD\] are alternate angles and for two parallel lines, alternate angles are equal to each other. It means \[\angle ACD\] and \[\angle CAB\] is equal to each other
\[\angle ACB=\angle CAD\] ………………….(2)
Adding equation (1) and equation (2), we get
\[\angle ACD+\angle ACB=\angle CAB+\angle CAD\] ……………..(3)
Now, \[\angle A\] can be written as the summation of \[\angle CAD\] and \[\angle CAB\] .
\[\angle A=\angle CAB+\angle CAD\] …………………….(4)
Similarly, \[\angle C\] can be written as the summation of \[\angle ACB\] and \[\angle ACD\].
\[\angle C=\angle ACD+\angle ACB\] ……………………..(5)
Now, using equation (4) and equation (5), we can simplify equation (3)
\[\begin{align}
  & \angle ACD+\angle ACB=\angle CAB+\angle CAD \\
 & \Rightarrow \angle C=\angle A \\
\end{align}\]
Therefore, \[\angle A-\angle C=0\] .
Hence, option (C) is the correct one.

Note: We can also solve this question by taking an ideal parallel. Let’s assume a square. We know that every square is a parallelogram. In a square, all angles are equal, and each angle measures \[{{90}^{0}}\].
So, the difference between \[\angle A\] and \[\angle C\] is zero because both angles are equal.