Question

In a parallelogram, opposite angles are equal. Now, is the converse of this result also true$?$Yes.
Using the angle sum of a quadrilateral and the result of parallel lines intersected by a transversal.

Answer 1

Hint: In these above statements, we show that if it's two diagonals are identified along with any of their intersecting angles, the converse of triangle we can also determine the area of a parallelogram, the area of any parallelogram can also be determined using its diagonal lengths. As we know, a parallelogram has two diagonals which intersect each other.

Formula used:
The sum of the interior angles in a quadrilateral is 360 degrees.
Parallelogram Area Using Sides,
\[{{Area = Base \times Height}}\]
${{A = b \times h }}\,{\text{square}}\,{\text{unit}}$
Parallelogram Area Without Height,
\[{{Area}} = ab\,\sin \left( x \right)\]
Parallelogram Area Using Diagonals,
\[Area = \dfrac{1}{2}{\text{ }} \times {{\text{d}}_1} \times {d_2}\,\sin \left( y \right)\]
Where,
$b = $ base of the parallelogram $\left( {AB} \right)$
$h = $height of the parallelogram
$a = $side of the parallelogram $\left( {AD} \right)$
$x = $any angle between the sides of the parallelogram \[(\angle DAB{\text{ }}or\angle ADC)\]
${d_1} = $diagonal of the parallelogram \[\left( p \right)\]
${d_2}$$ = $diagonal of the parallelogram \[\left( q \right)\]
$y = $any angle between at the intersection point of the diagonals \[(\angle DOA{\text{ }}or\angle DOC)\]

Complete step-by-step answer:
Given opposite angles are equal and that the converse is also true,
We find the result of parallel lines intersected by a transversal,
The parallelogram given below,

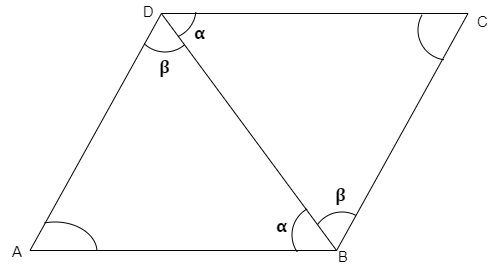
We know that two congruent triangles of parallelogram is $\left| \!{\underline {\,
  A \,}} \right. = \left| \!{\underline {\,
  C \,}} \right. $
Let as join \[B\] to $D$
We get,
The pair of alternate triangles
$\left| \!{\underline {\,
  {ABD} \,}} \right. $ and $\left| \!{\underline {\,
  {BCD} \,}} \right. $
Also $AB||DC$and $DC$ is a traversal
Let the know the property of the parallelogram,
The alternate pair of triangles are
$\left| \!{\underline {\,
  A \,}} \right. = \left| \!{\underline {\,
  C \,}} \right. $
When
\[AB||CD\] are parallel
$\left| \!{\underline {\,
  {ABD} \,}} \right. = \left| \!{\underline {\,
  {CDB} \,}} \right. $
Then,
$AD||CB$ are parallel
$\left| \!{\underline {\,
  {ADB} \,}} \right. = \left| \!{\underline {\,
  {CBD} \,}} \right. $
Here ASA of parallelogram
$\Delta ABC \cong \Delta CBD$
 Hence, The theorem Diagonal AC divides parallelogram $ABCD$ into two congruent triangles $ABD$ and $CBD$
Now, measure the opposite sides of parallelogram ABCD.
By concept of \[AB{\text{ }} = {\text{ }}DC\] and \[AD{\text{ }} = {\text{ }}BC\].

Note: The parallelogram's base and height are opposite to each other, while the base is not opposite to the lateral side of the parallelogram. The opposite sides are equal in size and the opposite angles are equal in way of measuring in a parallelogram.