Question

In a parallelogram $ ABCD, $ the bisector of angle $ ABC $ intersect $ AD $ at $ P. $ If $ PD = 5,BP = 6 $ and $ CP = 6 $ , find $ AB $
(A) $ 5 $
(B) $ 4 $
(C) $ 6 $
(D) $ 8 $

Answer 1

Hint: Use the properties of parallelogram and similarity of triangles to solve this question.

Complete step-by-step answer:
Observe the diagram

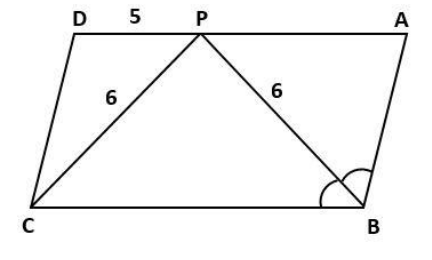
 $ \Delta PBC $ is an isosceles triangle.
 $ \because PB = CP = 6 $ (Given)
Also, $ \angle PBC = \angle APB $ (alternate interior angles) . . . (1)
 $ \angle PBC = \angle ABP $ (Since, PB is angle bisector) . . . (2)
From equation (1) and (2), we get
 $ \angle APB = \angle ABP $
 $ \Rightarrow \Delta APB $ is an isosceles triangle.
 $ \Rightarrow AP = AB $ (Sides opposite to equal angles of isosceles triangle)
In $ \Delta PCB $ and $ \Delta APB $
 $ \angle PBC = \angle PBA $ (Since, PB is angle bisector) . . . (3)
From equation (3) and the fact that $ \Delta PCB $ and $ \Delta APB $ are isosceles triangle. We can say that
 $ \angle PCB = \angle APB $ (Since their opposite angles are equal to each other)
Since, two angles of two triangles are equal, there third angle must be equal as well.
 $ \Rightarrow \angle CPB = \angle PAB $
Therefore, by AAA criteria of similarity of triangles, we can write
 $ \Delta PCB \approx \Delta APB $
Therefore, by the property of similar triangles, the ratio of corresponding sides of the two triangles is equal
 $ \Rightarrow \dfrac{{PC}}{{AP}} = \dfrac{{CB}}{{PB}} = \dfrac{{PB}}{{AB}} $
\[ \Rightarrow \dfrac{{CB}}{{PB}} = \dfrac{{PB}}{{AB}}\]
 $ BC = AD $ (Opposite sides of a parallelogram)
\[ \Rightarrow \dfrac{{AD}}{{PB}} = \dfrac{{PB}}{{AB}}\]
 $ AD = AP + PD $
\[ \Rightarrow \dfrac{{AP + PD}}{{PB}} = \dfrac{{PB}}{{AB}}\]
 $ AP = AB $ (Opposite sides to equal angles of $ \Delta APB $ )
\[ \Rightarrow \dfrac{{AB + PD}}{{PB}} = \dfrac{{PB}}{{AB}}\]
\[ \Rightarrow \dfrac{{AB + 5}}{6} = \dfrac{6}{{AB}}\] $ (\because PD = 5 $ and $ PB = 6) $
By cross multiplying, we get
 $ A{B^2} + 5AB = 36 $
Let $ AB = x $
Then we get
 $ {x^2} + 5x = 36 $
By rearranging it, we get
 $ \Rightarrow {x^2} + 5x - 36 = 0 $
This is a quadratic equation. We will solve it by splitting the middle term
 $ \Rightarrow {x^2} + 9x - 4x - 36 = 0 $
 $ \Rightarrow x(x + 9) - 4(x + 9) = 0 $
 $ \Rightarrow (x + 9)(x - 4) = 0 $
 $ \Rightarrow x = - 9,4 $
But length cannot be negative.
Therefore $ x = 4 $
 $ \therefore AB = AP = 4 $
Therefore, the value of $ AB = 4 $

So, the correct answer is “Option B”.

Note: In this question, less information was given directly. We had to find out the information we needed to solve this question using the properties of parallelogram, isosceles triangle and similarity of two triangles. From this question, we understand that properties of geometrical figures are very important.