Question

In a parallelogram $ABCD$ if angle $D = 125^\circ $, then the other angles are?

Answer 1

Hint: Parallelogram is a four sided figure whose opposite sides are parallel to each other. Also, the opposite sides of a parallelogram are equal to each other in length. The opposite angles of a parallelogram are also equal to each other. And the sum of all the angles of a parallelogram is $360^\circ $. For example, let $PQRS$ be a parallelogram, so,
$PQ = RS$ and $PS = QR$
[Opposite sides of a parallelogram are equal]
$\angle P = \angle R$, $\angle Q = \angle S$ and $\angle P + \angle Q + \angle R + \angle S = 360^\circ $
[Opposite angles of a parallelogram are equal and the sum of all the angles is $360^\circ $]

Complete step by step answer:
Given a parallelogram $ABCD$ and one of it’s angles, $\angle D = 125^\circ $.
Now, we know, the opposite sides of a parallelogram are equal.
Therefore, $\angle A = \angle C$ and $\angle B = \angle D$.

So, $\angle B = \angle D = 125^\circ $
Also, we know that, the sum of all the angles of a parallelogram is $360^\circ $.
So, $\angle A + \angle B + \angle C + \angle D = 360^\circ $
Substituting, the angles $\angle B$ and $\angle D$, we get,
$ \Rightarrow \angle A + 125^\circ + \angle C + 125^\circ = 360^\circ $
$ \Rightarrow \angle A + \angle C + 250^\circ = 360^\circ $
Subtracting $250^\circ $ from both sides of equation, we get,
$ \Rightarrow \angle A + \angle C = 360^\circ - 250^\circ $
$ \Rightarrow \angle A + \angle C = 110^\circ $
As we have seen above, $\angle A = \angle C$.
Substituting this in the equation above, we get,
$ \Rightarrow 2\angle A = 110^\circ $
$ \Rightarrow \angle A = 55^\circ $
Therefore, $\angle C = \angle A = 55^\circ $
Therefore, the angles of the parallelogram are,
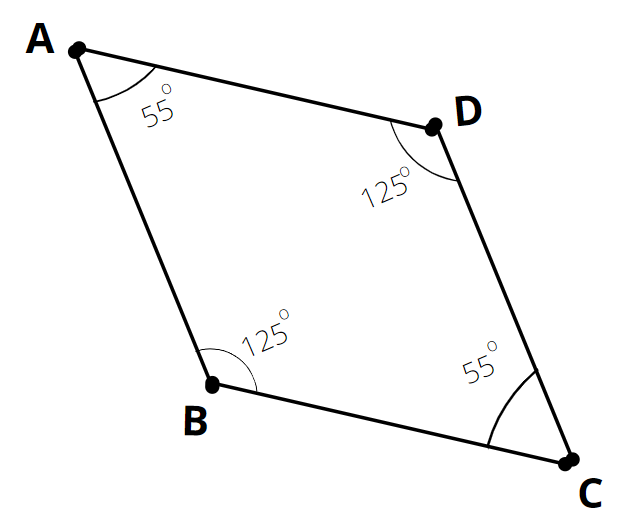
$\angle A = 55^\circ $, $\angle B = 125^\circ $, $\angle C = 55^\circ $, $\angle D = 125^\circ $
These angles are represented in the following diagram

Note:
A parallelogram is the origin for a lot of shapes, it is the most basic shape, which when modified in special ways for various other kinds of shapes. Like, when all the angles of a parallelogram are equal to $90^\circ $, it is called a rectangle. When all the sides of a parallelogram are equal, it is called a rhombus. And, when all the sides of a parallelogram are equal and also, all the angles of the parallelogram are equal to $90^\circ $, it is called a square.