Question

In a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.

Answer 1

Hint: A parallelogram had four sides and two pairs of parallel sides, in the solution it is given that the E and F are the midpoints then we can conclude they are equal to each other and according to the parallel statements we can show the line segments AF and EC trisect the diagonal BD.

Complete step-by-step answer:
Given:
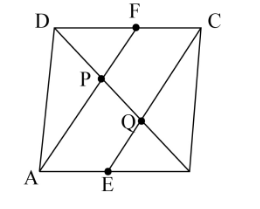
ABCD is a parallelogram.
E and F are the midpoints of the sides AB and DC.
In a parallelogram, we can say that\[AB//CD\], Then the opposite sides are equal so
\[\Rightarrow AB = CD\].
We know that point E is the midpoint one the AB and F is the midpoint on the CD, then it can be said that \[AE = CF\].
The sides AF and CE are parallel to each other and\[AE = CF\], Then AECF is parallelogram.
We can observe P and Q are the points on the lines AF and CE
According to it PF is parallel to CQ and AP parallel to EQ where these AF and CE are touching at three points each.
Now according to the parallel sides, the point P is midpoint of DQ and point Q is midpoint of BP.
Then, \[\Rightarrow PQ = DP\]--assuming as equation 1
\[\Rightarrow PQ = BQ\]--assuming as equation 2
From the two equations, it can be convey that \[PQ = BQ = DP\]
As these equality (\[PQ = BQ = DP\]) is because of the diagonal BD, then we can say that the line segments AF and EC trisect the diagonal BD.
Therefore, the required statement is shown.

Note: Here while we assuming anything, we have to be about it whether the statements are according to the rules and theorems of a parallelogram, in this we can show the required statement by taking the triangles CDQ and ABP and proving one of the sides is equal to the other.