Question

In a parallelogram ABCD, $ |AB| = a,\,\,|AD| = b\,\,and\,\,|AC| = c $ . Then, DB. AB has the value
 $
  A.\,\,\,\dfrac{{3{a^2} + {b^2} - {c^2}}}{2} \\
  B.\,\,\,\dfrac{{{a^2} + 3{b^2} - {c^2}}}{2} \\
  C.\,\,\,\dfrac{{{a^2} - {b^2} + 3{c^2}}}{2} \\
  D.\,\,\,\dfrac{{{a^2} + 3{b^2} + {c^2}}}{2} \\
  $

Answer 1

Hint: To find required value we will use the concept of triangle law in triangle ADB to form an equation and then using property of parallelogram to form another equation and then solving two formed equations together to derive the required result or solution of given problem.

Complete step-by-step answer:
Given
In parallelogram ABCD, we have $ |AB| = a,\,\,|AD| = b\,\,and\,\,|AC| = c $

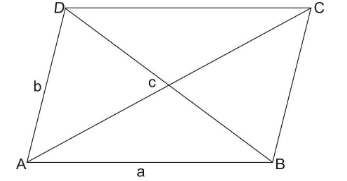
Since ABCD is a parallelogram. Therefore, values of sides BC and CD will be given as:
 $ |BC| = |AD| = b $ and
 $ |CD| = |AB| = a $
In triangle ABD by triangle law we have
 $ BD = BA + AD $
Or we can write it as
 $ AD = BA - BD $
Squaring both sides. We have,
 $
  {(AD)^2} = {\left( {BA - BD} \right)^2} \\
   \Rightarrow {\left( {AD} \right)^2} = {(BA)^2} + {\left( {BD} \right)^2} - 2.BA.BD \\
  or\,\,we\,\,can\,\,write\,\,above\,\,equation\,as: \\
  |AD{|^2} = |AB{|^2} + |BD{|^2} - 2AB.DB \;
  $
Substituting value in above. We have,
 $ {b^2} = {a^2} + |BD{|^2} - 2AB.DB................(i) $
Also, we know that in a parallelogram twice the sum of squares of two sides is equal to the sum of squares of its diagonal.
Therefore, we have:
 $ 2\left( {|AB{|^2} + |AD{|^2}} \right) = |AC{|^2} + |BD{|^2} $
Substituting values in above. We have,
 $
  2\left( {{a^2} + {b^2}} \right) = {c^2} + |BD{|^2} \\
  or\,\,we\,\,can\,\,write\,\,it\,\,as: \\
  |BD{|^2} = 2{a^2} + 2{b^2} - {c^2}..................(ii) \\
  $
Using (ii) in (i). We have,
 $
  {b^2} = {a^2} + 2{a^2} + 2{b^2} - {c^2} - 2AB.DB \\
   \Rightarrow 2AB.DB = 3{a^2} + {b^2} - {c^2} \\
   \Rightarrow AB.DB = \dfrac{{3{a^2} + {b^2} - {c^2}}}{2} \;
  $
Therefore, the required value of $ DB.AB $ is $ \dfrac{{3{a^2} + {b^2} - {c^2}}}{2} $ .
So, the correct answer is “Option A”.

Note: We can also find the solution of a given problem by using the concept of scalar dot product. In this we find dot product between sides $ DB\,\,and\,\,AB $ and then find the value of cosine of the angle between then we use triangle formula of cosine angle to write its value and then using this value back in equation to find require value or solution of given problem.