Question

In a non right angled triangle $ \Delta PQR $ , let p, q, r denote the lengths of sides opposite to the angles at P, Q, R respectively. The median from R meets the sides PQ at S, the perpendicular 4 from P meets the side QR at E, and RS and PE intersect at O. If p = $ \sqrt{3} $ , q = 1 and radius of the circumcircle of the $ \Delta PQR $ equals 1, then which of the following options is/are correct?
(a) length of RS= $ \dfrac{\sqrt{7}}{2} $
(b) Area of $ \Delta SOE=\dfrac{\sqrt{3}}{12} $
(c) Radius of incircle of $ \Delta PQR=\dfrac{\sqrt{3}}{2}\left( 2-\sqrt{3} \right) $
(d) Length of OE= $ \dfrac{1}{6} $

Answer 1

Hint: We will apply sine rule formula which is given by $ \dfrac{p}{\sin A}=\dfrac{q}{\sin B}=\dfrac{r}{\sin C} $ where the alphabets A, B and C represents individual angles of a triangle and p, q, r are the sides of the triangle. We will also apply the median formula which is given by $ \dfrac{1}{2}\sqrt{2\left( \text{first side of}\,\Delta \right)+2\left( \text{second}\,\text{side of }\Delta \right)-\left( \text{third side of }\Delta \right)} $
The third side is basically the side whose length we need to find out. Also, we will use area of triangle’s formula which is given by $ \text{Area of triangle}=\dfrac{1}{2}\times \,\text{base}\times n\sin \left( \theta \right) $ where $ n\sin \left( \theta \right) $ is the height of the triangle.

Complete step-by-step answer:
According to the question we need to consider a triangle $ \Delta PQR $ with lengths of the sides opposite to the angles at P, Q, R respectively. This implies that the front of angle P will be named as QR. Then QR = p. Similarly, sides PQ and RS with the lengths r and s respectively as shown below

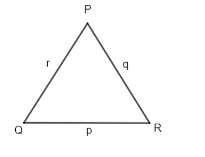
Now, draw the median from R which meets the sides PQ at S, the perpendicular 4 from P which meets the side QR at E, and RS and PE intersect at O as shown below. Along with it we draw a circumcircle of a triangle. It means a circle which touches all three vertices of a triangle. Accordingly a circum circle with radius 1 unit of $ \Delta PQR $ is a circle which touches all vertices. This is shown below.

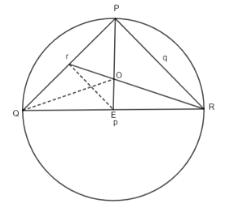
Now, we use the sine rule to the angles of the triangle. Therefore, we have
 $ \dfrac{p}{\sin P}=\dfrac{q}{\sin Q}=\dfrac{r}{\sin R}=2{{R}_{1}} $ where $ {{R}_{1}} $ represents radius of the circle. Now, we will substitute values p = $ \sqrt{3} $ , q = 1 and $ {{R}_{1}} $ = 1 in (i). Thus, we get
 $ \begin{align}
  & \dfrac{p}{\sin P}=\dfrac{q}{\sin Q}=\dfrac{r}{\sin R}=2{{R}_{1}} \\
 & \Rightarrow \dfrac{\sqrt{3}}{\sin P}=\dfrac{1}{\sin Q}=\dfrac{r}{\sin R}=2\times 1 \\
 & \Rightarrow \dfrac{\sqrt{3}}{\sin P}=\dfrac{1}{\sin Q}=\dfrac{r}{\sin R}=2 \\
\end{align} $
Now, we will compare $ \dfrac{\sqrt{3}}{\sin P}=2,\dfrac{1}{\sin Q}=2,\dfrac{r}{\sin R}=2 $ . Therefore, we have
 $ \sin P=\dfrac{\sqrt{3}}{2},\sin Q=\dfrac{1}{2} $ and $ \sin R=\dfrac{r}{2}...(ii) $ .
We know that $ \sin \left( \dfrac{\pi }{3} \right)=\dfrac{\sqrt{3}}{2} $ . Thus, we have $ \sin P=\sin \left( \dfrac{\pi }{3} \right) $ or $ P=\dfrac{\pi }{3} $ . Also, we know $ \sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2} $ . Therefore, we get
 $ \begin{align}
  & \sin Q=\dfrac{1}{2} \\
 & \Rightarrow \sin Q=\sin \left( \dfrac{\pi }{6} \right) \\
 & \Rightarrow q=\dfrac{\pi }{6} \\
\end{align} $
The values of P and Q are under $ {{90}^{\circ }} $ second value of $ \sin P=\dfrac{\sqrt{3}}{2} $ is $ \sin \left( P=\dfrac{2\pi }{3} \right)=\dfrac{\sqrt{3}}{2} $ . Thus, $ P=\dfrac{2\pi }{3} $ . Also,
 $ \begin{align}
  & \sin Q=\dfrac{1}{2} \\
 & \Rightarrow \sin Q=\sin \dfrac{5\pi }{6} \\
 & \Rightarrow q=\dfrac{5\pi }{6} \\
\end{align} $
Clearly, we get $ P=\dfrac{\pi }{3},\dfrac{2\pi }{3} $ and $ Q=\dfrac{\pi }{6},\dfrac{5\pi }{6} $ . We know that the sum of all interior angles of a triangle is $ {{180}^{\circ }} $ . This results into the use of ‘hit and trial method’. In this case we will make pairing of the angles such that the third angle also fits in this sum. For example, we can have one condition that will satisfy (ii) $ \left( \dfrac{\pi }{3},\dfrac{\pi }{6} \right),\left( \dfrac{\pi }{3},\dfrac{5\pi }{6} \right),\left( \dfrac{2\pi }{3},\dfrac{5\pi }{6} \right),\left( \dfrac{2\pi }{3},\dfrac{\pi }{6} \right) $ in ordering dine as (P, Q). We will first consider
 $ \begin{align}
  & \dfrac{\pi }{3}+\dfrac{\pi }{6}+R={{180}^{\circ }} \\
 & \Rightarrow \dfrac{2\pi +\pi }{6}+R={{180}^{\circ }} \\
 & \Rightarrow \dfrac{3\pi }{6}+R={{180}^{\circ }} \\
 & \Rightarrow R={{180}^{\circ }}-\dfrac{3\pi }{6} \\
\end{align} $
We know that $ {{180}^{\circ }}=\pi $ . Therefore,
 $ \begin{align}
  & R=\pi -\dfrac{3\pi }{6} \\
 & \Rightarrow R=\dfrac{6\pi -3\pi }{6} \\
 & \Rightarrow R=\dfrac{3\pi }{6} \\
 & \Rightarrow R=\dfrac{\pi }{2} \\
 & \Rightarrow R={{90}^{\circ }} \\
\end{align} $
This value will not be considered since in the question it is clearly written that the triangle cannot be a right angled triangle. Similarly, the pairs of $ \left( \dfrac{\pi }{3},\dfrac{5\pi }{6} \right) $ and $ \left( \dfrac{2\pi }{3},\dfrac{5\pi }{6} \right) $ are also cancelled. So, we are left with the value that is $ \left( \dfrac{2\pi }{3},\dfrac{\pi }{6} \right) $ . Thus, we get
 $ \begin{align}
  & P+Q+R=\pi \\
 & \Rightarrow \dfrac{2\pi }{3}+\dfrac{\pi }{6}+R=\pi \\
 & \Rightarrow R=\pi -\dfrac{2\pi }{3}-\dfrac{\pi }{6} \\
 & \Rightarrow R=\pi -\left( \dfrac{4\pi +\pi }{6} \right) \\
 & \Rightarrow R=\pi -\left( \dfrac{5\pi }{6} \right) \\
 & \Rightarrow R=\dfrac{6\pi -5\pi }{6} \\
 & \Rightarrow R=\dfrac{\pi }{6} \\
\end{align} $
Now, we will substitute this value in the equation (ii). Therefore, we get
 $ \begin{align}
  & \sin \left( R \right)=\dfrac{r}{2} \\
 & \Rightarrow \sin \left( \dfrac{\pi }{6} \right)=\dfrac{r}{2} \\
 & \because \sin \left( \dfrac{\pi }{6} \right)=\dfrac{1}{2} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{r}{2} \\
 & \Rightarrow r=1 \\
\end{align} $
By this we come to know that the side PQ is equal to 1. Now, we will take the median of RS. Since, it is the median on the side PQ of the triangle. By the formula we have
 $ \begin{align}
  & \text{length of the side RS=}\dfrac{1}{2}\sqrt{2{{\left( PR \right)}^{2}}+2{{\left( RQ \right)}^{2}}-P{{Q}^{2}}} \\
 & \Rightarrow \dfrac{1}{2}\sqrt{2{{\left( PR \right)}^{2}}+2{{\left( RQ \right)}^{2}}-P{{Q}^{2}}}=\dfrac{1}{2}\sqrt{2{{\left( 1 \right)}^{2}}+2{{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}}} \\
 & \Rightarrow \text{length of the side RS=}\dfrac{1}{2}\sqrt{2+6-1} \\
 & \Rightarrow \text{length of the side RS=}\dfrac{\sqrt{7}}{2} \\
\end{align} $
Hence, option (a) is the right option. After this we can either choose to solve option (c) but we cannot solve directly option (b). In option (c) we will find the radius of incircle of $ \Delta PQR $ . By the term in circle we mean a circle which lies inside the triangle touching all midpoints of side. By the formula of area of triangle we get,
 $ \begin{align}
  & \text{area of triangle = inradius }\times \,\left( \dfrac{\text{sum of sides of }\Delta }{2} \right) \\
 & \Rightarrow \text{inradius = area of triangle }\times \,\left( \dfrac{2}{\text{sum of sides of }\Delta } \right) \\
 & \Rightarrow \text{inradius = area of triangle }\times \,\left( \dfrac{2}{p+q+r} \right) \\
 & \Rightarrow \text{inradius = }\dfrac{\text{product of sides}}{\text{4 radius of circumcircle}}\text{ }\times \,\left( \dfrac{2}{p+q+r} \right) \\
\end{align} $
This is done by formula $ \text{area of triangle = }\dfrac{\text{product of sides}}{\text{4 radius of circumcircle}} $
 $ \begin{align}
  & \Rightarrow \text{inradius = }\dfrac{p\times q\times r}{\text{4 }\left( 1 \right)}\text{ }\times \,\left( \dfrac{2}{p+q+r} \right) \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}\times 1\times 1}{\text{4}}\text{ }\times \,\left( \dfrac{2}{\sqrt{3}+1+r} \right) \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\text{ }\times \,\dfrac{1}{\left( \sqrt{3}+2 \right)} \\
\end{align} $
Now, we will use rationalization here multiplying numerator and denominator by $ 2-\sqrt{3} $ , we get
 $ \begin{align}
  & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\text{ }\times \,\dfrac{1}{\left( \sqrt{3}+2 \right)}\times \dfrac{2-\sqrt{3}}{2-\sqrt{3}} \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\text{ }\times \,\dfrac{2-\sqrt{3}}{{{\left( 2 \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}} \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\text{ }\times \,\dfrac{2-\sqrt{3}}{4-3} \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\text{ }\times \,\dfrac{2-\sqrt{3}}{1} \\
 & \Rightarrow \text{inradius = }\dfrac{\sqrt{3}}{2}\left( 2-\sqrt{3} \right) \\
\end{align} $
Hence, option (c) is the correct option.
Now, we will find the value of the length of OE. It is possible by the formula
 $ \begin{align}
  & \text{OE }\!\!'\!\!\text{ s length}=\dfrac{2\left( \text{area of }\Delta \text{PQR} \right)}{QR} \\
 & \because \text{area of }\Delta \text{OQR=}\dfrac{1}{2}\times \text{base}\times \text{height} \\
 & \Rightarrow \text{area of }\Delta \text{OQR=}\dfrac{1}{2}\times \text{QR}\times \text{OE} \\
 & \Rightarrow \text{the length of OE=}\dfrac{2\left( \text{area of }\!\!\Delta\!\!\text{ OQR} \right)}{\text{QR}} \\
\end{align} $
Here one cannot say the value of $ \Delta OQR $ .But if we find the value of area of $ \Delta PQR $ then by the relation of $ \text{area of }\Delta OQR=\dfrac{1}{3}\times \text{area of }\Delta \text{PQR} $ we can solve it. Now, we will find the value of the area of $ \Delta PQR $ . It is given by $ \dfrac{1}{2}\times \text{base}\times \text{height} $ . That is, $ \begin{align}
  & \text{area of }\!\!\Delta\!\!\text{ PQR=}\dfrac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ QR }\!\!\times\!\!\text{ PE} \\
 & \Rightarrow \text{area of }\!\!\Delta\!\!\text{ PQR=}\dfrac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ QR }\!\!\times\!\!\text{ sin}\left( {{30}^{\circ }} \right)\times \text{PQ}....(iii) \\
\end{align} $
This is done because PE is not directly given to us so by angle $ Q={{30}^{\circ }} $ we can find $ \begin{align}
  & \sin \left( {{30}^{\circ }} \right)=\dfrac{\text{perpendicular}}{\text{hypotenuse}} \\
 & \Rightarrow \sin \left( {{30}^{\circ }} \right)=\dfrac{PE}{PQ} \\
 & \Rightarrow \sin \left( {{30}^{\circ }} \right)\times PQ=PE \\
\end{align} $
By the equation we get after substituting PQ = 1 and QR = $ \sqrt{3} $ .
 $ \text{area of }\Delta \text{PQR=}\dfrac{1}{2}\times \sqrt{3}\times 1\times \sin \left( {{30}^{\circ }} \right) $
Since, we know that the value of $ \sin \left( {{30}^{\circ }} \right)=\dfrac{1}{2} $ . Therefore, we have
 $ \begin{align}
  & \text{area of }\Delta \text{PQR=}\dfrac{1}{2}\times \sqrt{3}\times 1\times \sin \left( {{30}^{\circ }} \right) \\
 & \Rightarrow \text{area of }\Delta \text{PQR=}\dfrac{1}{2}\times \sqrt{3}\times 1\times \dfrac{1}{2} \\
 & \Rightarrow \text{area of }\Delta \text{PQR=}\dfrac{\sqrt{3}}{4} \\
\end{align} $
Now, we substitute this value in equation $ \text{the length of OE=}\dfrac{2\left( \text{area of }\!\!\Delta\!\!\text{ OQR} \right)}{\text{QR}} $ which is further equal to,
 $ \begin{align}
  & \text{the length of OE=}\dfrac{2\left( \dfrac{1}{3}\times \text{area of }\!\!\Delta\!\!\text{ OQR} \right)}{\text{QR}} \\
 & \Rightarrow \text{the length of OE=}\dfrac{2\left( \dfrac{1}{3}\times \dfrac{\sqrt{3}}{4} \right)}{\sqrt{3}} \\
 & \Rightarrow \text{the length of OE=}\dfrac{1}{6} \\
\end{align} $
Hence, option (d) is the correct option.
Now, we will verify whether the value of $ \text{area of }\Delta \text{SOE=}\dfrac{\sqrt{3}}{12} $ or not. We know that $ \text{area of }\Delta \text{SOE=}\dfrac{1}{2}\times \text{base}\times \text{height} $ and the base of the triangle is SE.

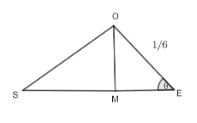
By the diagram the height of $ \Delta SOE=OM $ and OM can be written in terms of $ \sin \left( \theta \right)=\dfrac{\text{perpendicular}}{hypotenuse} $ . Thus, we have
 $ \begin{align}
  & \sin \left( \theta \right)=\dfrac{OM}{OE} \\
 & \Rightarrow \sin \left( \theta \right)=\dfrac{OM}{\left( \dfrac{1}{6} \right)} \\
 & \Rightarrow \sin \left( \theta \right)\times \dfrac{1}{6}=OM \\
\end{align} $
Now, in this case we don’t know the value of $ \theta $ yet. So, we use the fact “if a triangle is inside a circumcircle, let’s say we have the same diagram as in this question, then $ \angle QPR=\angle QOR $ “. By using this we have $ \angle QPR=\angle QOR={{120}^{\circ }} $ and,
 $ \begin{align}
  & \angle QPE=\angle QOE=\dfrac{1}{2}\left( {{120}^{\circ }} \right) \\
 & \Rightarrow \angle QPE=\angle QOE={{60}^{\circ }} \\
\end{align} $ .
Since, M is a median on SE so it divides SE into two equal lengths as well as it divides $ \angle SOE $ into equal angles. Thus, $ \angle QPE=\angle QOE={{60}^{\circ }} $ results into exactly of itself if a median is drawn from it. In this case we have a median OM on SE. So, $ \angle QOE={{30}^{\circ }} $ . And we know $ \angle OME={{90}^{\circ }} $ . Therefore, by using the fact that all the sum of inner angles of a triangle is equal to $ {{180}^{\circ }} $ . Thus, we have
 $ \begin{align}
  & \angle OME+\angle MOE+\angle OEM={{180}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+{{30}^{\circ }}+\angle OEM={{180}^{\circ }} \\
 & \Rightarrow \angle OEM={{180}^{\circ }}-{{90}^{\circ }}-{{30}^{\circ }} \\
 & \Rightarrow \angle OEM={{60}^{\circ }} \\
\end{align} $
Therefore, we have that $ \theta ={{60}^{\circ }} $ . By this we have that $ OM=\dfrac{1}{6}\sin \left( {{60}^{\circ }} \right) $ . Since, $ \sin \left( {{60}^{\circ }} \right)=\dfrac{\sqrt{3}}{2} $ . Thus, we get
 $ \begin{align}
  & OM=\dfrac{1}{6}\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow OM=\dfrac{\sqrt{3}}{12} \\
\end{align} $
This is our height of a triangle. Substituting the values of OM and the base SE we get,
 $ \begin{align}
  & \text{area of }\Delta \text{SOE=}\dfrac{1}{2}\times SE\times OM \\
 & \Rightarrow \text{area of }\Delta \text{SOE=}\dfrac{1}{2}\times \dfrac{1}{2}\left( PR \right)\times OM \\
 & \Rightarrow \text{area of }\Delta \text{SOE=}\dfrac{1}{2}\times \dfrac{1}{2}\times 1\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow \text{area of }\Delta \text{SOE=}\dfrac{\sqrt{3}}{48}\,\text{uni}{{\text{t}}^{2}} \\
\end{align} $
Hence, option (b) is a wrong option.
Hence, the required answer is (a), (c), (d).

Note: In this equation the order of the options is (a), (b), (c), (d). Basically, we are talking about the length of RS followed by the area of $ \Delta SOE $ . But no one can find out $ \Delta SOE $ directly unless we find the radius of incircle and length of OE. So, the ordered way as given in the option to solve does not always follow. While applying the sine rule it should not be implied that the triangle given to us is isosceles or equilateral. It is decided by the degree only. As we know the basic formula of the area of the triangle but in this case the height is not given to us. So, we applied here, $ \text{area of triangle =}\dfrac{1}{2}\times \text{base}\times \left( \text{side}\times \sin \left( \theta \right) \right) $ . To understand it better we have applied this area of the triangle to $ \Delta SOE $ .