Question

In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 minutes after he starts playing. What is the probability that the music will stop within the first half-minute after starting?
(a) 1
(b) \[\dfrac{1}{2}\]
(c) \[\dfrac{1}{8}\]
(d) \[\dfrac{1}{4}\]

Answer 1

Hint:Draw a diagram in which the length of the musical track is 2 units and the length of half minute track is \[\dfrac{1}{2}\] units. Now, probability can be calculated by the ratio of the length of full-length track and length of the half-minute musical track.

Complete step-by-step answer:
According to the question, it is given that in a musical chair game, a person who is playing the music has been advised to stop playing the music at any time within 2 minutes after he starts playing. We have to find the probability that the music will stop within the first half-minute after the start of the musical chair game.
Let us visualize the length of the musical track using a distance type diagram. Since it has been advised to stop playing music at any time within 2 minutes. So, we can say that the length of the musical track is 2 minutes.

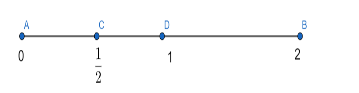
As shown in the figure, the distance AB equal to 2 units is the full length of the musical track which is equal to 2 minutes.
AB = 2 units …………….(1)
We have to find the probability that the music will stop within the first half-minute after starting. It means that this time the length of the music track is half minutes.
As shown in the figure, the distance AC equal to \[\dfrac{1}{2}\] units is the required length of the musical track which is equal to half minutes.
AC = \[\dfrac{1}{2}\] units ………………..(2)
The probability that music stops after half minutes = \[\dfrac{\text{Length of half minute musical track}}{\text{Full length of the musical track}}\]
The probability that music stops after half minutes = \[\dfrac{\dfrac{1}{2}}{2}=\dfrac{1}{4}\] .
Therefore, the probability that the music will stop within the first half-minute after starting is \[\dfrac{1}{4}\] .
Hence, the correct option is (d).

Note: In this question, one might make a mistake in understanding the word “ first-half minute”. One might think of it as “first and half a minute”. Both mean different things. The first half is the time duration of half-minute from the start. The first and half a minute is 1.5 minutes from the start. So, keep this point in mind.