Question

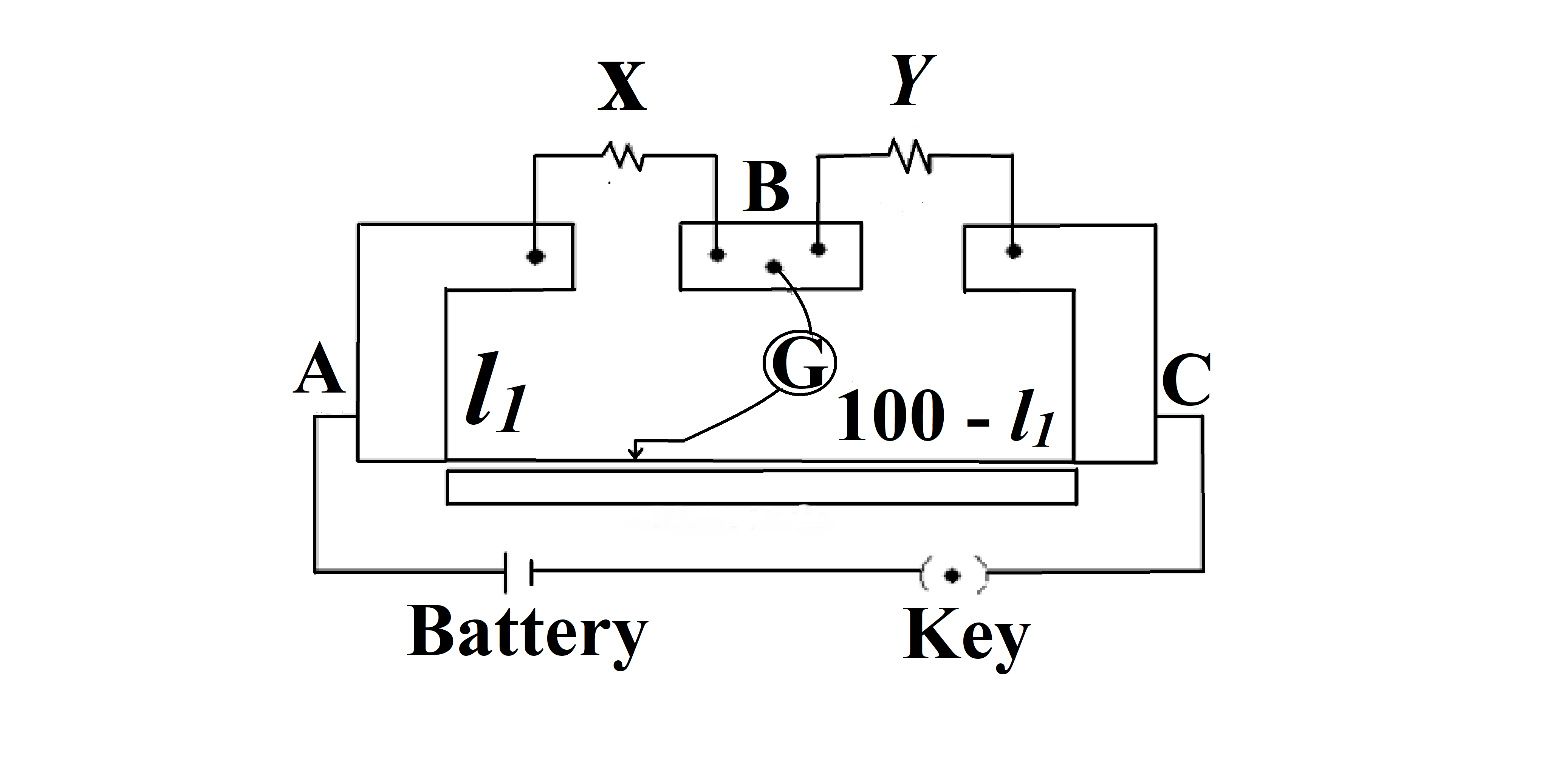
In a meter bridge, as shown in the figure, it is given that resistance \[Y=12.5\Omega \] and that balance is obtained at distance 39.5 cm, from the end A (by the jockey J). After interchanging the resistances X and Y, a new balance point is found at a distance ${{l}_{2}}$ from end A. What are the values of X and ${{l}_{2}}$?

Answer 1

Hint: A meter bridge, also known as a slide wire bridge, is an instrument that functions on the Wheatstone bridge principle. A meter bridge is used to describe a conductor 's uncertain resistance as that of a Wheatstone bridge, which was invented in 1843 by The Wheatstone bridge was invented by Samuel Hunter Christie. We can solve this question using the meter bridge formula.
Formula used:
For solving this question, we will be using the formula for the meter bridge, i.e.,
$X=Y\dfrac{l}{(100-l)}$

Complete answer:
Before solving the question, let us take a look at the given parameters
$X=12.5\Omega $
$l=39.5cm$
By using the values given above, we can find the value of the other resistance, i.e., Y
So,
$X=Y\dfrac{l}{(100-l)}$
$\Rightarrow 12.5=Y\times \dfrac{39.5}{(100-39.5)}$
$\Rightarrow X=12.5\times \dfrac{60.5}{39.5}$
$\Rightarrow X=8.16\Omega $
Now, we have the values of both X and Y, so moving on to the second part
The resistances are interchanged


Again, applying the same method
We have,
$Y=X\dfrac{{{l}_{2}}}{(100-{{l}_{2}})}$
$\Rightarrow \dfrac{12.5}{8.16}=\dfrac{{{l}_{2}}}{(100-{{l}_{2}})}$
$\Rightarrow 1.53(100-{{l}_{2}})={{l}_{2}}$
$\Rightarrow \dfrac{153}{2.53}={{l}_{2}}$
$\Rightarrow {{l}_{2}}=60.5cm$
So after solving, we have the values
$X=8.16\Omega $
${{l}_{2}}=60.5cm$

Note:
The reason why we subtract the length of the balance point by 100 is because the meter bridge is 100 cm long (or 1 m long as the name suggests itself). The meter bridge works on the theory that the ratio of resistances is equal to the ratio of their corresponding lengths, i.e., distance of the balance point from their respective sides.