Question

In a hydraulic lift used at a service station, the radius of the large and the small piston are in ratio of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg?
$\begin{array}{l}
{\rm{A}}{\rm{. 3}}{\rm{.75}}kg\\
{\rm{B}}{\rm{. 37}}{\rm{.5}}kg\\
{\rm{C}}{\rm{. 7}}{\rm{.5}}kg\\
{\rm{D}}{\rm{. 75}}kg
\end{array}$

Answer 1

Hint: We know that the Pascal law states that the pressure applied at one point of the liquid is transmitted equally in all the directions of the liquid. Using the relation between pressures for small and big piston, we can calculate the force required to lift the weight of the car.

Formula used:
Pascal’s law is given as
\[{P_1} = {P_2}\]
Here ${P_1}$ and ${P_2}$ are the pressure applied by the same fluid.
Pressure is defined as
$P = \dfrac{F}{A}$
Here F represents the force applied on the fluid while A is the area over which the force is applied.

Complete step-by-step answer:
We are given a hydraulic lift which works on the principle of Pascal’s law. According to this law, when a certain amount of pressure is applied on a given liquid, it gets transmitted equally throughout the whole liquid.
A hydraulic lift uses this principle where we apply pressure from one end which gets transmitted to the other end. It has two pistons, one with larger radius and other with smaller radius. The weight that is to be lifted is placed on the larger piston which can be lifted by applying force on the smaller piston.

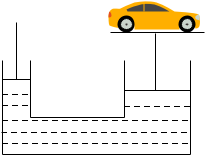
We are given the ratio of the radius of the large and the small piston. If ${r_1}$ is the radius of the large piston and ${r_2}$ is the radius of the small piston, the ratio is given as
$\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{20}}{1}$
The car is placed on the larger piston. The weight of the car is given as
${W_1} = 1500kg$
Now we need to find out the force that must be applied on the smaller piston in order to lift the weight of the car. For this, we will use Pascal's law as given in equation (i) in the following way.
Pressure applied on the larger piston is equal to the pressure applied on the smaller piston.
\[\begin{array}{l}
{P_1} = {P_2}\\
\dfrac{{{W_1}}}{{\pi r_1^2}} = \dfrac{{{W_2}}}{{\pi r_2^2}}\\
 \Rightarrow {W_2} = \dfrac{{r_2^2}}{{r_1^2}}{W_1}
\end{array}\]
Now we will use the values that are already given. Doing so we obtain the force required to be
\[{W_2} = {\left( {\dfrac{1}{{20}}} \right)^2} \times 1500 = 3.75kg\]
This is the required answer. Hence, the correct answer is option A.

Note:The student should note that the same pressure does not mean that same amount of force is required. Because of the different areas of the piston, we need a weight of just 3.75 kg in order to lift a car which is as heavy as 1500 kg.