Question

In a hot water heating system, there is a cylindrical pipe of length 28m and diameter 5cm. Find the total radiating surface area in the system.

Answer 1

 Hint:The total radiating surface area means that we have to calculate the total surface area. The water heating system is in the form of a cylinder so use the direct formula for the total surface area of the cylinder which is $T.S.A = C.S.A + \left( {2 \times {A_C}} \right)$.

Complete step by step answer:

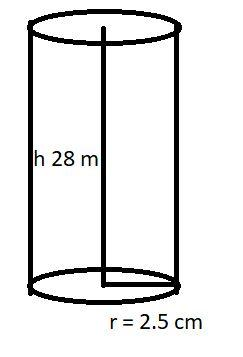
The diagram of a hot water heating system having cylindrical pipe is shown above.
The length (l) or height (h) of the cylindrical pipe = 28 m (see figure).
Now as we know that 1m =100cm
Therefore height (h) of cylinder is = 2800 cm
The diameter is 5 cm.
As we know that the radius (r) is half of the diameter.
$ \Rightarrow r = \dfrac{5}{2} = 2.5$ cm (see figure).
Now we have to find out the total radiating surface in the system.
So the total radiating surface in the system is nothing but the total surface area (T.S.A) of the cylindrical pipe.
Now as we know that the T.S.A of the cylindrical pipe is the sum of curved surface area (C.S.A) and the area (AC) of two circular ends.
$ \Rightarrow T.S.A = C.S.A + \left( {2 \times {A_C}} \right)$
Now as we know C.S.A of the cylinder is $\left( {2\pi rh} \right)$ and the area of the circular end is $\left( {\pi {r^2}} \right)$.
$ \Rightarrow T.S.A = 2\pi rh + \left( {2 \times \pi {r^2}} \right)$ Square unit.
Now substitute all the values in this equation we have,
$ \Rightarrow T.S.A = 2 \times \dfrac{{22}}{7} \times 2.5 \times 2800 + \left( {2 \times \dfrac{{22}}{7} \times {{\left( {2.5} \right)}^2}} \right)$ cm2 $\left[ {\because \pi = \dfrac{{22}}{7}} \right]$
Now simplify this equation we have,
$ \Rightarrow T.S.A = 44000 + 39.28 = 44039.28{\text{ c}}{{\text{m}}^2}$
So this is the required radiating surface in the system.

Note – Let’s talk about why the radiating surface of a water heating system is total surface and not the curved surface area. For this we learned the difference between curved surface area and total surface area. In T.S.A the two circular bases are also included whereas in curved surface areas these two bases are excluded, that’s why the formula of T.S.A is the sum of C.S.A and the area of two circular bases. Now the radiations must have escaped from the circular bases too thus we are concerned about the total surface area.