Question

In a group of 52 people,16 read Taranga but not Sudha and 33 read Taranga. How many read Sudha but not Taranga?
A. 19
B. 20
C. 30
D. 23

Answer 1

Hint: Draw a venn diagram for representing the number of people who are speaking Taranga and Sudha. Use variables to represent the parts of the venn-diagram.
Now, use the given information and form equations in terms of the variables and hence solve them to get the values of variables. Finally calculate the required answer from the Venn-diagram.

Complete step-by-step answer:
Here, we have a group of 52 people in which 16 read Taranga but not Sudha and 33 read Taranga, and we need to determine the number of people who read Sudha but not Taranga.
We can solve this question by drawing a Venn diagram with the relation of people who read Taranga and Sudha.
So, let us have two circles denoting the number of people reading Taranga and Sudha and some people who read both are also shown.

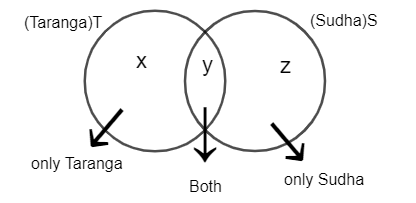
Let, there are x, y, z people lying in the three parts of the above diagram. So,
X is denoting people who are reading Taranga but not Sudha.
Z is denoting people who are reading Sudha but not Taranga.
Y is denoting people who are reading both Sudha and Taranga.
Now, we have a total number of people as 52. So, 52 people will contain people who read only Sudha, both and Taranga as per the Venn-diagram. So, we get
\[x+y+z=52\] …………………………………………..(i)
Now, it is also given that 16 read Taranga only but not Sudha, so 16 people will lie in Taranga part of the venn diagram. It means the value of x is 16. So, we get
$x=16$ …………………………………………………..(ii)
Now, another condition is that 33 read Taranga. It means 33 people will belong to the whole circle of the Taranga(venn-diagram) which is represented by T in the figure. So, $\left( x+y \right)$ people will read Taranga from the diagram; so, we get
$x+y=33$ ………………………………………………….(iii)
Now, put the value of $\left( x+y \right)$ from equation (iii) to equation (i). So, we get
$33+z=52$
$z=52-33=19$ people
And put the value of x from equation (ii) to equation (iii) to get the value of y. So, we get
\[16+y=33\]
$y=33-16=17$ people
So, we get $x=16,y=17,z=19$
Now, we can draw our venn diagram as

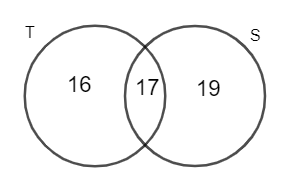
Now, coming to the question, it is asked to find the number of people who read Sudha but not Taranga.
So, we can observe the above venn diagram and get the answer as 19 which is the value of variable z.
Hence, 19 people are there who read Sudha but not Taranga.
So, option (A) is correct.

Note: Another approach for calculating the number of people who read Sudha not Taranga as :-
We know
$n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)$
Hence, we get
$\Rightarrow n\left( S\cup T \right)=n\left( S \right)+n\left( T \right)-n\left( S\cap T \right)$
$n\left( S \right)\to $ People who read Sudha
$n\left( T \right)\to $ People who read Taranga
$n\left( S\cap T \right)\to $ People who read both
$n\left( S\cup T \right)\to $ Total people involved to read Sudha or Taranga.
Hence, $n\left( S\cup T \right)=52$
$n\left( T \right)=33$
And, we have $n\left( T \right)-n\left( S\cap T \right)=16$ i.e. people who read Taranga not Sudha.
$n\left( S\cap T \right)=33-16=17$
Now, find $n\left( S \right)$ from the above mentioned formula and $n\left( S \right)-n\left( T\cap S \right)$ i.e. people who read Sudha not Taranga. Now, solve it.
Venn diagrams are the most powerful and fundamental approach for these kinds of questions. It makes understanding of questions much better than any other method. And be careful while using the above mentioned method in ‘Note’.