Question

In a group of 36 girls, each one can stitch or weave or do both. If 25 girls can stitch and 17 girls can stitch only, how many can weave only?

Answer 1

Hint: This is a problem of set theory. We will form two sets such that one represents the number of girls who stitch and the other represents the number of girls which weave. We will first construct a Venn Diagram for these two sets. We have been given the total number of girls, those who stitch, and those who stitch only. We will assign these values on the Venn diagram to compute the number of girls who can weave only.

Complete step-by-step answer:
We have been given that there are a total of 36 girls. Let the number of girls who stitch be represented by a set A, and those who weave be represented by a set B. We can plot these on the Venn diagram as-

The common region between the two sets is ${\text{A}} \cap {\text{B}}$, which is the number of girls who stitch and weave both. We have been given that the number of girls that stitch are
n(A) = 25. Also, the number of girls who stitch only will equal to the difference of the number of girls who stitch and those who stitch and weave both. This can be calculated as-
$\begin{align}
  &{\text{n}}\left( {{\text{A}} - {\text{B}}} \right) = {\text{n}}\left( {\text{A}} \right) - {\text{n}}\left( {{\text{A}} \cap {\text{B}}} \right) \\
  &{\text{n}}\left( {{\text{A}} \cap {\text{B}}} \right) = {\text{n}}\left( {\text{A}} \right) - {\text{n}}\left( {{\text{A}} - {\text{B}}} \right) \\
  &{\text{n}}\left( {{\text{A}} \cap {\text{B}}} \right) = 25 - 17 = 8 \\
\end{align} $
Now, we will find the number of girls which weave using the formula for the total number of girls as-
$\begin{align}
  &{\text{n}}\left( {{\text{A}} \cup {\text{B}}} \right) = {\text{n}}\left( {\text{A}} \right) + {\text{n}}\left( {\text{B}} \right) - {\text{n}}\left( {{\text{A}} \cap {\text{B}}} \right) \\
  &36 = 25 + {\text{n}}\left( {\text{B}} \right) - 8 \\
  &{\text{n}}\left( {\text{B}} \right) = 36 - 25 + 8 = 19 \\
\end{align} $
But n(B) is the number of girls that weave, including those which can do weaving and stitching both. We need to find the girls who weave only. So, we will subtract n(B) by the number of girls who weave and stitch both, that has been calculated as 8-
$\begin{align}
  &{\text{n}}\left( {{\text{B}} - {\text{A}}} \right) = {\text{n}}\left( {\text{B}} \right) - {\text{n}}\left( {{\text{A}} \cap {\text{B}}} \right) \\
  &{\text{n}}\left( {{\text{B}} - {\text{A}}} \right) = 19 - 8 = 11 \\
\end{align} $
These are the number of girls which can weave only. The Venn diagram can now be drawn as-

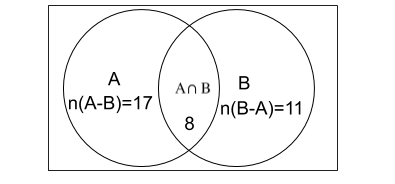
This is the required answer.

Note: An alternative method to solve this problem without using any formula is using the Venn diagram only. We just need to find the number of elements in each of the three regions using the data that has been given to us. Once we have those numbers, we can find any data that has been asked to find in the question.