Question

In a gravity free space, a man of mass M standing at a height h above the floor, throws a ball towards the ground. When the ball reaches the floor, the distance of the man above the floor will be:
A. $h\left( 1+\dfrac{m}{M} \right)$
B. $h\left( 2-\dfrac{m}{M} \right)$
C. 2h
D. a function of m, M, h and u

Answer 1

Hint: We will consider the ball and the man as one system. As there are no external forces, there would be no change in the centre of mass of the system. So, we will derive the formula for the centre of mass and then find the distance the man must have moved for the centre of mass to remain unchanged.
Formula used:
Position of centre of mass
$\dfrac{{{x}_{1}}{{m}_{1}}+{{x}_{2}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Complete step by step answer:
First as both the objects are at a height h above the ground, that will be their centre of mass as can be confirmed by using the formula for the position of centre of mass
$\dfrac{{{x}_{1}}{{m}_{1}}+{{x}_{2}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
Here ${{x}_{1}}$and ${{m}_{1}}$are the distance of the object from origin (can be chosen arbitrarily) and the mass of the object respectively for the first object and ${{x}_{2}}$and ${{m}_{2}}$are the distance of the object from origin (same as for the first one) and the mass of the object respectively for the second object.
Here when we enter the values of the required quantities, we get the centre of mass to be at a distance of $\dfrac{xM+hm}{M+m}=h$ from the origin, which here we will choose as the floor.
When the ball reaches the floor, the centre of mass will be at the same distance from the floor, but the man would have moved some distance. Let’s call the distance moved by the man to be x. Then,

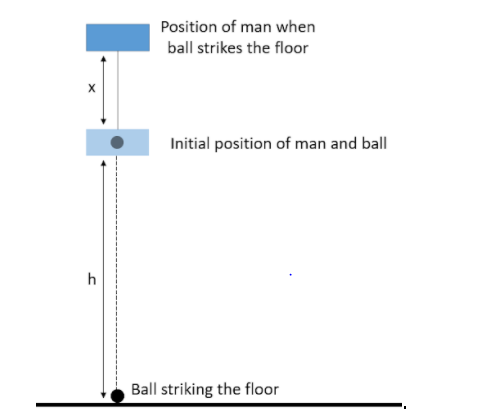
$\begin{align}
  & \dfrac{xM+(0)m}{M+m}=\dfrac{xM}{M+m}=h \\
 & \Rightarrow x=\dfrac{h\left( M+m \right)}{M}=h\left( 1+\dfrac{m}{M} \right) \\
\end{align}$
Hence, the correct option is A, i.e. $h\left( 1+\dfrac{m}{M} \right)$

Note:

We can also solve this question by considering the law of conservation of momentum. We will assume both the ball and man to have gained some velocity and then using the two equations for the momentum conservation and the velocity of the ball to be equal to the ratio of h and t, the time taken by the ball to reach ground. $MV=mv$and $v=\dfrac{h}{t}$. When we replace the value of v in first equation, we get
$M\dfrac{x}{t}=m\dfrac{h}{t}\Rightarrow x=\dfrac{mh}{M}$. This distance moved away from the floor, when we add its initial height, we get the same result. Take care we cannot use the first method for time after the ball strikes the floor as at that moment external force from the floor will act and the position of centre of mass will change.