Question

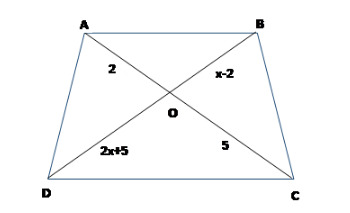
In a given figure in trapezium ABCD If AB||CD then value of x is-

A.\[\dfrac{{29}}{8}\]
B.\[\dfrac{8}{{29}}\]
C.\[20\]
D.\[\dfrac{1}{{20}}\]

Answer 1

Hint: Given figure in trapezium ABCD If AB||CD. In the given diagram we draw a line say EF parallel to AB and DC as well as passing through 0. Diagonals AC and BD intersect at O. we can find the value of x by showing that\[\dfrac{{AO}}{{BO}} = \dfrac{{CO}}{{DO}}\]. (Parallel on a plane will never meet). Now we will prove this.

Complete step-by-step answer:
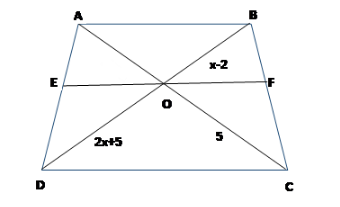
Constructing a line parallel to AB and BC. Passing through O. AS show in the figure.
Now, consider\[\Delta \]\[ADC\],
We can see that EO is parallel to DC.
\[EO||DC\] (Because\[EF||DC\],)
So, \[ \Rightarrow \dfrac{{AE}}{{DE}} = \dfrac{{AO}}{{CO}}\] ----- (1)
Because, a line drawn parallel to one side of a triangle, intersects the other two sides in distinct points, then it divides the other 2 sides in the same ratio.

Similarly,
In\[\Delta \]\[DBA\], we have \[EO||AB\] (Because\[EF||AB\]).
So, \[ \Rightarrow \dfrac{{AE}}{{DE}} = \dfrac{{BO}}{{DO}}\] ----- (2)
Because, a line drawn parallel to one side of a triangle, intersects the other two sides in distinct points, then it divides the other 2 sides in the same ratio.
From (1) and (2) we have,
\[ \Rightarrow \dfrac{{AO}}{{CO}} = \dfrac{{BO}}{{DO}}\]
\[ \Rightarrow \dfrac{{AO}}{{BO}} = \dfrac{{CO}}{{DO}}\].
We have\[AO = 2\], \[BO = x - 2\], \[CO = 5\]and \[DO = 2x + 5\].
Substituting, we get:
\[ \Rightarrow \dfrac{2}{{x - 2}} = \dfrac{5}{{2x + 5}}\]
\[ \Rightarrow 2(2x + 5) = 5(x - 2)\]
\[ \Rightarrow 4x + 10 = 5x - 10\]
\[ \Rightarrow 5x - 4x = 10 + 10\]
\[ \Rightarrow x = 20\]
So, the correct answer is “x=20”.

Note: The ration that proved in above is a theorem. We have proved it here. They can also ask only the theorem part. To solve this question if you know the theorem you can solve it directly. Do it depending on the marks that are assigned to it. In trapezium the opposite lines are always parallel to each other.