Question

In a given figure \[\angle 3,\angle 4\]are exterior angles in a quadrilateral \[ABCD\]at point \[B\]and \[D\] and \[\angle A = \angle 2,\angle C = \angle 1\]. Prove that \[\angle 3 + \angle 4 = \angle 1 + \angle 2\]

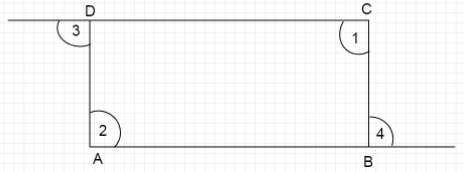
Answer 1

Hint:We prove this by writing the angles on the line having the sum \[{180^ \circ }\]and using the concept of sum of all angles in a quadrilateral is \[{360^ \circ }\] we make an equation of all angles of quadrilateral.
* Angles are measured in degrees or radians.

Complete step-by-step answer:
Let us denote the remaining two angles of the quadrilateral by \[\angle 5,\angle 6\]

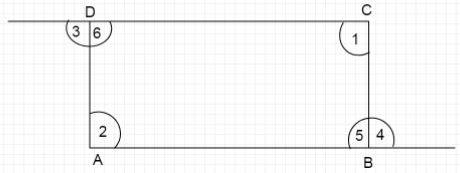
Now since we know sum of angles on a straight line is \[{180^ \circ }\]
At point \[B\], \[\angle 5 + \angle 4 = {180^ \circ }\]
Therefore, we can write \[\angle 5 = {180^ \circ } - \angle 4\] \[...(i)\]
At point \[D\], \[\angle 3 + \angle 6 = {180^ \circ }\]
Therefore, we can write \[\angle 6 = {180^ \circ } - \angle 3\] \[...(ii)\]
Now take the quadrilateral \[ABCD\] having sides \[AB,BC,CD,DA\] and angles \[\angle 1,\angle 2,\angle 5,\angle 6\].
Since, we know sum of all interior angles of a quadrilateral sum to \[{360^ \circ }\]
Therefore, we can write sum of all angles of quadrilateral \[ABCD\]as
\[\angle 1 + \angle 2 + \angle 5 + \angle 6 = {360^ \circ }\]
We now substitute the values of \[\angle 5,\angle 6\]in this equation from equations \[(i),(ii)\]
\[\angle 1 + \angle 2 + ({180^ \circ } - \angle 4) + ({180^ \circ } - \angle 3) = {360^ \circ }\]
Opening the brackets and adding the values in the LHS of the equation.
\[\angle 1 + \angle 2 - \angle 4 - \angle 3 + {180^ \circ } + {180^ \circ } = {360^ \circ }\]
\[\angle 1 + \angle 2 - \angle 4 - \angle 3 + {360^ \circ } = {360^ \circ }\]
Shift all the degree values to RHS of the equation.
\[\angle 1 + \angle 2 - \angle 4 - \angle 3 = {360^ \circ } - {360^ \circ }\]
\[\angle 1 + \angle 2 - \angle 4 - \angle 3 = {0^ \circ }\]
Take negative sign common and group together \[\angle 3,\angle 4\]
\[\angle 1 + \angle 2 - (\angle 4 + \angle 3) = {0^ \circ }\]
Shift the negative bracket to the right side of the equation to make it positive.
\[\angle 1 + \angle 2 = \angle 4 + \angle 3\]
Hence Proved.

Note:Alternative method:
We draw a diagonal \[AC\] in the diagram which breaks the angles \[\angle 1,\angle 2\] in two parts each respectively.
Therefore, \[\angle 1,\angle 2\] can be written as
\[\angle 1 = \angle ACD + \angle ACB\]
\[\angle 2 = \angle CAD + \angle CAB\]

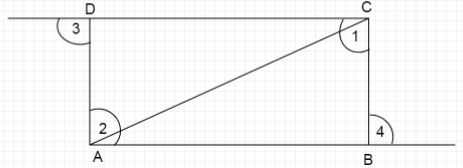
Now, using the property of exterior angles of a triangle, we know Exterior angle is equal to the sum of opposite interior angles.
Here \[\angle 3,\angle 4\] are the exterior angles.
Here, In \[\vartriangle ABC\] , \[\angle 4 = \angle CAB + \angle ACB\]
Also, in \[\vartriangle ADC\], \[\angle 3 = \angle CAD + \angle ACD\]
Now, calculate the sum \[\angle 3 + \angle 4\]
\[\angle 3 + \angle 4 = (\angle CAD + \angle ACD) + (\angle CAB + \angle ACB)\]
                  \[ = \angle CAD + \angle ACD + \angle CAB + \angle ACB\]
Now grouping the angles in such a way that they sum up to form angles \[\angle 1,\angle 2\]
\[\angle 3 + \angle 4 = (\angle CAD + \angle CAB) + (\angle ACD + \angle ACB)\]
Substituting the values \[\angle 4 = \angle CAB + \angle ACB\] and \[\angle 3 = \angle CAD + \angle ACD\]
\[\angle 3 + \angle 4 = \angle 2 + \angle 1\]
Hence Proved.