Question

In a face-centered lattice with all the positions occupied by A atoms, the body-centered octahedral holes in it are occupied by an atom B of an appropriate size for such a crystal. Predict the formula of the compound.
(A) AB
(B) ${{A}_{4}}B$
(C) ${{A}_{4}}{{B}_{3}}$
(D) ${{A}_{4}}{{B}_{5}}$

Answer 1

Hint: To solve this question we first need to know what is a crystal cubic system. A crystal system in which the shape of the unit cell is a cube is known as a crystal cubic system. The three main types of these crystals are face-centered, body-centered, and primitive cubic.

Complete answer:
Now, in a body-centered cubic system (cl), there is one lattice point on the corner of each unit along with a lattice point at the center of the cube.

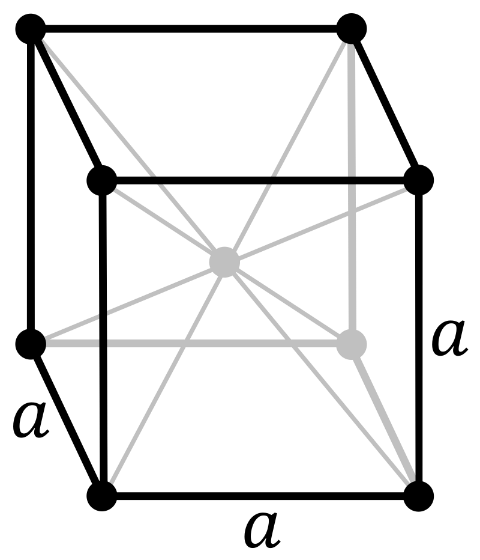
So the number of atoms in the unit cell will be
\[(\dfrac{1}{8}\times 8)+1=2\]
It has 6 net octahedral voids and 12 net tetrahedral voids.
In a face-centered cubic system (cF), there is one lattice point on the corner of each unit along with a lattice point at the center of the faces of the cube (which given $\dfrac{1}{2}$ atom contribution).

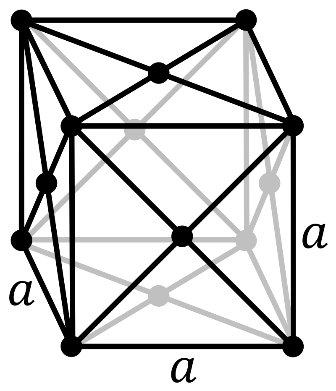
So, the number of atoms in the unit cell will be
\[(\dfrac{1}{8}\times 8)+(\dfrac{1}{2}\times 6)=4\]
It has 4 net octahedral voids and 4 net tetrahedral voids.
So, the number of atoms of A = 4 as it occupies lattice points in a face-centered unit.
And the number of atoms of B = 4 as it occupies octahedral voids in a body-centered unit.

So, the formula of the compound will be ${{A}_{4}}{{B}_{4}}$ or option (A) AB.

Note:
It should be noted that in a primitive cubic system (cP), there is one lattice point on the corner of each unit. Since the atom at the lattice point is shared by all the 8 adjacent sides of the cube.

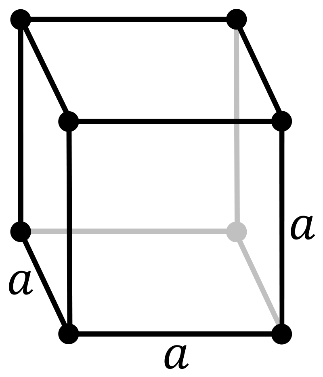
So, the number of atoms in the unit cell will be
\[\dfrac{1}{8}\times 8=1\]
It has a single cubic void in the center.