Question

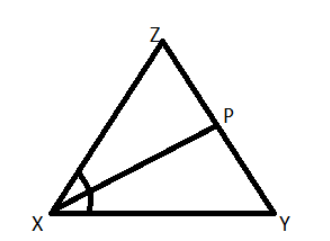
In a $\Delta XYZ$, if the internal bisector of angle X meets YZ at ‘P’, then……
$
  {\text{A}}{\text{.}}\dfrac{{{\text{XY + XZ}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YZ}}}}{{{\text{PZ}}}} \\
  {\text{B}}{\text{.}}\dfrac{{{\text{XY}}}}{{{\text{PZ}}}}{\text{ = }}\dfrac{{{\text{XZ}}}}{{{\text{YP}}}} \\
  {\text{C}}{\text{.}}\dfrac{{{\text{XY}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{PZ}}}}{{{\text{YP}}}} \\
  {\text{D}}{\text{.}}\dfrac{{{\text{XZ}}}}{{{\text{XY}}}}{\text{ = }}\dfrac{{{\text{YP}}}}{{{\text{PZ}}}} \\
$

Answer 1

Hint – In order to get the right answer to this problem we need to use angle bisector theorem and solve accordingly to get anyone of the provided options then we will get the right answer.

Complete step-by-step answer:
We can clearly see from the diagram that the internal angle bisector of X meets YZ at P.
We can say from angle bisector theorem that $\dfrac{{{\text{XY}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YP}}}}{{{\text{PZ}}}}$.
In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle as done above.
So, we have $\dfrac{{{\text{XY}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YP}}}}{{{\text{PZ}}}}$.
Adding 1 to both sides of the equation we get,
$
  \dfrac{{{\text{XY}}}}{{{\text{XZ}}}}{\text{ + 1 = }}\dfrac{{{\text{YP}}}}{{{\text{PZ}}}}{\text{ + 1}} \\
  \dfrac{{{\text{XY + XZ}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YP + PZ}}}}{{{\text{PZ}}}} \\
  \dfrac{{{\text{XY + XZ}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YZ}}}}{{{\text{PZ}}}} \\
$
Hence we got $\dfrac{{{\text{XY + XZ}}}}{{{\text{XZ}}}}{\text{ = }}\dfrac{{{\text{YZ}}}}{{{\text{PZ}}}}$ after solving which is nothing nut option A.
So, the correct option is A.

Note – Here we have a triangle with one of its angles bisected. Here we need to think of the property we can use to get any of the options provided. Here we have used the angle bisector theorem. Then solved it further to get the right answers. An angle bisector divides the opposite side of a triangle into two segments that are proportional to the triangle's other two sides.