Question

In a \[\Delta \] ABC, the line segments AD, BE and CF are three altitudes. If R is the circumradius of the \[\Delta \] ABC, then a side of the \[\Delta \] DEF will be
A. Rsin2A
B. cosB
C. asinA
D. bcosB

Answer 1

Hint: Draw a diagram of the given situation. Now, consider the triangle DEC and use the cosine formula given as \[\cos C=\dfrac{C{{D}^{2}}+C{{E}^{2}}-D{{E}^{2}}}{2CD.CE}\]. To determine the value of side CD and CE consider the right triangles ADC and BEC one by one. Use the substitution $CD=b\cos C$ and $CE=a\cos C$. Here a, b and c are the sides of the triangle ABC opposite to the angles A, B and C respectively. Find the value of DE using these substitutions and then use the cosine formula in triangle ABC given as $\cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$ to find the length of side DE in terms of c and $\cos C$. Once the pattern is formed, find the length of the other two sides DF and EF. Check the option which is correct. Use the formulas: $a=2R\sin A$, $b=2R\sin B$ and $c=2R\sin C$ to find more relations and to check if any more options can be correct.

Complete step by step solution:
Here we have been provided with a triangle ABC and its altitudes AD, BE and CF. A triangle DEF is formed and we need to determine the options which correctly depict the sides of the triangle DEF. First let us draw a diagram of the given situation.

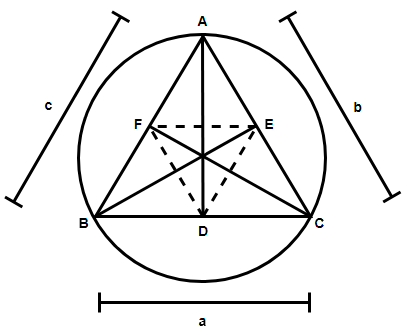
Now, in the above figure we have considered a, b and c as the sides opposite to the angles A, B and C respectively. In triangle CED we can use the cosine formula given as:
\[\Rightarrow \cos C=\dfrac{C{{D}^{2}}+C{{E}^{2}}-D{{E}^{2}}}{2CD.CE}........\left( i \right)\]
Let us determine the sides CD and CE in terms of the sides of triangle ABC and its angles. So we have,
(1) In right triangle ADC we have,
AC = b = hypotenuse, CD = base (considering the angle C)
\[\begin{align}
  & \Rightarrow \cos C=\dfrac{CD}{AC} \\
 & \Rightarrow \cos C=\dfrac{CD}{b} \\
 & \Rightarrow CD=b\cos C........\left( ii \right) \\
\end{align}\]
(2) In right triangle BEC we have,
BC = a = hypotenuse, CE = base (considering the angle C)
\[\begin{align}
  & \Rightarrow \cos C=\dfrac{CE}{BC} \\
 & \Rightarrow \cos C=\dfrac{CE}{a} \\
 & \Rightarrow CE=a\cos C........\left( iii \right) \\
\end{align}\]
Substituting the values of CD and CE from equations (ii) and (iii) respectively in equation (i) we get,
\[\begin{align}
  & \Rightarrow \cos C=\dfrac{{{\left( b\cos C \right)}^{2}}+{{\left( a\cos C \right)}^{2}}-D{{E}^{2}}}{2\left( b\cos C \right)\left( a\cos C \right)} \\
 & \Rightarrow \cos C=\dfrac{{{b}^{2}}{{\cos }^{2}}C+{{a}^{2}}{{\cos }^{2}}C-D{{E}^{2}}}{2ab{{\cos }^{2}}C} \\
\end{align}\]
By cross multiplication we get,
\[\begin{align}
  & \Rightarrow 2ab{{\cos }^{3}}C={{b}^{2}}{{\cos }^{2}}C+{{a}^{2}}{{\cos }^{2}}C-D{{E}^{2}} \\
 & \Rightarrow D{{E}^{2}}={{b}^{2}}{{\cos }^{2}}C+{{a}^{2}}{{\cos }^{2}}C-2ab{{\cos }^{3}}C \\
 & \Rightarrow D{{E}^{2}}={{\cos }^{2}}C\left( {{a}^{2}}+{{b}^{2}}-2ab\cos C \right)........\left( iv \right) \\
\end{align}\]
Now, let us come to the triangle ABC. Using the cosine formula for angle C we get,
\[\begin{align}
  & \Rightarrow \cos C=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} \\
 & \Rightarrow 2ab\cos C={{a}^{2}}+{{b}^{2}}-{{c}^{2}} \\
 & \Rightarrow {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos C \\
\end{align}\]
So using the above obtained relation we can write the equation (iv) as:
\[\begin{align}
  & \Rightarrow D{{E}^{2}}={{\cos }^{2}}C\left( {{c}^{2}} \right) \\
 & \Rightarrow D{{E}^{2}}={{c}^{2}}{{\cos }^{2}}C \\
 & \Rightarrow D{{E}^{2}}={{\left( c\cos C \right)}^{2}} \\
\end{align}\]
Taking square root both the sides we get,
\[\Rightarrow DE=c\cos C\]
Now let us see the obtained expression carefully. We can see that when we have considered the side DE of triangle DEF which is opposite to the angle C then we get \[DE=c\cos C\], so when we will consider the side DF which is opposite to angle B we will get $DF=b\cos B$ and similarly for the side EF which is opposite to the angle A we will get $EF=a\cos A$. So the three sides can be given as:
$\therefore EF=a\cos A,DF=b\cos B$ and \[DE=c\cos C\].
Clearly option (d) is correct. Now, we have been given that R is the circum – radius of the triangle ABC and we have three relations between the sides, angles and the circum – radius given as: $a=2R\sin A$, $b=2R\sin B$ and $c=2R\sin C$. Therefore, we can write the side DE as:
\[\Rightarrow DE=2R\sin C\cos C\]
Using the identity $2\sin x\cos x=\sin 2x$ we get the above relation as:
\[\Rightarrow DE=R\sin 2C\]
Similarly the other two sides will be $EF=R\sin 2A$ and $DF=R\sin 2B$. Clearly option (a) is also correct.
Hence our answers are options (a) and (d).

Note: If the question is objective type with options provided just like in the above case there is a very easy method to determine the correct options. What you can do is assume the triangle as an equilateral triangle whose circumcenter, orthocenter, incenter, centroid all lie on the same point. Consider angles A, B and C each equal to 60 degrees and assume all the sides as ‘a’. Now, the triangle DEF will also become an equilateral triangle with each side measuring $\dfrac{a}{2}$ according to Thales' theorem. Substitute the values of angles in the options and simplify their sine or cosines whatever present and check in which cases we get the side length as $\dfrac{a}{2}$. However we cannot apply this method in subjective type questions.