Question

In a $\Delta $ ABC, D and E are points on AB and AC respectively such that $DE||BC$ . If AD=2.4cm, AE = 3.2cm, DE = 2cm and BC = 5cm, Find BD and CE.

Answer 1

Hint: Consider $\Delta ADE,\Delta ABC$ , prove that the triangles are similar by A.A similarity criteria. Then the corresponding sides of both triangles are also similar. Thus substitute and find BD and CE.

Complete step-by-step answer:

Let us draw $\Delta ABC$ , let us mark points D and E on the sides AB and AC of the $\Delta ABC$ . It is said that $DE||BC$ , we have been given the sides as AD = 2.4cm, DE = 2cm, AE = 3.2cm and BC=5cm.

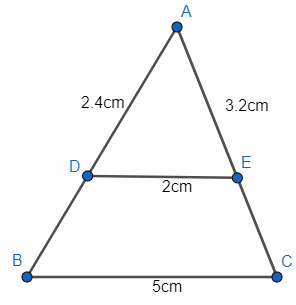
So let us find the length of AB and AC first. Thus, from the figure,

$\begin{align}

  & AB=AD+BD\Rightarrow BD=AB-AD.........................\left( i \right) \\

 & AC=AE+EC\Rightarrow CE=AC-AE........................\left( ii \right) \\

\end{align}$

So, from the figure let us first consider $\Delta ADE,\Delta ABC$ it is said that $DE||BC$ . Thus we can say that

$\begin{align}

  & \angle ADE=\angle ABC \\

 & \angle AED=\angle ACB \\

\end{align}$

Corresponding angles means that 2 angles correspond by being on the same side of the transversal. Thus by AA similarity postulates, the same side of two triangle are congruent, then $\Delta ADE,\Delta ABC$ are similar

i.e $\Delta ADE\cong \Delta ABC$

Hence we can say that as the triangles are similar, their corresponding sides are proportional. Thus we can write,

$\dfrac{AE}{AC}=\dfrac{AD}{AB}=\dfrac{DE}{BC}$

Now, let us consider the value of AE = 3.2cm, AD = 2.5cm, DE = 2cm and BC = 5cm,

$\therefore \dfrac{3.2}{AC}=\dfrac{2.5}{AB}=\dfrac{2}{5}$

Now let us equate

$\dfrac{3.2}{AC}=\dfrac{2}{5},\dfrac{2.5}{AB}=\dfrac{2}{5}$

Now apply cross multiplication property on both the equation and get the value of AB and AC.

$\begin{align}

  & 2AC=5\times 3.2 \\

 & \Rightarrow AC=\dfrac{5\times 3.2}{2}=5\times 1.6=8cm \\

 & 2AB=2.4\times 5 \\

 & \Rightarrow AB=\dfrac{2.4\times 5}{2}=5\times 1.2=6cm \\

\end{align}$

Hence we got AC = 8cm and AB = 6cm. Now, put these values in equation (i) and (ii)

BD = AB – AD = 6 – 2.4 = 3.6cm

CE = AC- AE = 8 – 3.2 = 4.8cm

Hence we got BD = 3.6cm and CE = 4.8cm. Thus we got the required value.

Note: The AA similarity postulate is a shortcut for showing that two triangles are similar. If you know that two angles in one triangle are congruent to 2 angles in another, which is now enough information to show that the 2 triangles are similar. Then you can use the similarity to get the length of sides.