Question

In a \[\Delta ABC\], angle \[ABC\] is equal to twice the angle \[ACB\], and the bisector of angle \[ABC\] meets the opposite side at point \[P\]. Show that:
(i)$CB:BA = CP:PA$
(ii)$AB \times BC = BP \times CA$

Answer 1

Hint: In the first part, use the given conditions to prove that \[\angle ABP = \angle PBC\] and then apply angle bisector theorem to prove the relation, $CB:BA = CP:PA$. In the second part, prove that \[\Delta ABC \approx \Delta APB\] and then use the property of similarity to get the required relation, $AB \times BC = BP \times CA$.

Complete step-by-step answer:
Let us first draw the figure corresponding to the given conditions.

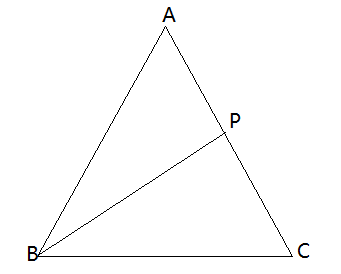
(i)Let us consider \[\Delta ABC\] and the \[\Delta APB\] from the figure,
Let \[\angle ACB = x\].
Then, according to given conditions, \[\angle ABC = 2\angle ACB = 2x\]
We are given that $BP$ is the bisector of \[\angle ABC\].
Hence, we have, \[\angle ABP = \angle PBC = x\]
Now, we will use the angle bisector theorem. Angle bisector theorem states that the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, $CB:BA = CP:PA$

(ii)Let us consider \[\Delta BPC\] from the figure,
Apply exterior angle property.
Exterior angle property states that, an exterior angle is equal to the sum of two opposite interior angles.
Hence, \[\angle APB = 2x\]
Also, \[\angle ABC = 2x\]
Therefore, we have \[\angle APB = \angle ABC\]
We are given that \[\angle BCP = \angle ABP\]
Also, \[\angle BAC = \angle BAP\] as it is the same angle.
Thus, \[\Delta ABC \approx \Delta APB\] by AAA criterion.
This implies that the ratio of corresponding sides is equal.
$\dfrac{{AB}}{{BP}} = \dfrac{{CA}}{{CB}}$
Hence, $AB \times BC = BP \times CA$

Note: Angle bisector theorem states that the bisector of an angle divides the side opposite to it in the ratio of other two sides. Exterior angle property states that, an exterior angle is equal to the sum of two opposite interior angles. Also, when angles are similar, the ratio of corresponding sides is equal.