Question

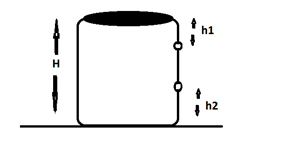
In a cylindrical water tank here are two small holes Q and P on a wall at a depth of ${h_1}$ from upper level of water and at a height of ${h_2}$ from a lower end of the tank , respectively, as shown in diagram. Water coming out of both the holes strikes the ground at the same point. The ratio of ${h_1}$ and ${h_2}$ is

$\left( A \right)1$
$\left( B \right)2$
$\left( C \right) > 1$
$\left( D \right) < 1$

Answer 1

Hint:The word efflux means fluid outflow. Apply the Torricelli equation to find the speed of efflux. Then apply the kinematic equation to determine its efflux velocity. Find the time taken by the efflux liquid to reach the floor. Apply the time equations in the kinematic equation to get the ratios of ${h_1}$and ${h_2}$.

Formula used:
$v = \sqrt {2gh} $
$s = ut + \dfrac{1}{2}a{t^2}$
Where $v$ is the efflux velocity, $h$ is the height of the cylinder, $a$ is the acceleration and $t$ is the time.

Complete step by step answer:
Consider a cylindrical water tank containing water with two holes at a position P and Q. P is placed at the height ${h_2}$from the ground level and Q is placed at height ${h_1}$from the top of the cylindrical tank. H is the height of the cylinder. Water coming from both holes P and Q strike the ground at the same point. By drawing a trajectory, we come to know its range is the same for both the liquids coming out the holes.
Now apply the Torricelli equation to the liquids coming out the holes. ${v_1}$ is the efflux velocity at point Q and ${v_2}$ is the efflux velocity at point P.
${v_1} = \sqrt {2g{h_1}} $
\[{v_2} = \sqrt {2g\left( {H - {h_2}} \right)} \]
We know that the range is same for the liquids coming out the holes
${R_1} = {R_2}$
Apply the kinematic equation $s = ut + \dfrac{1}{2}a{t^2}$.
No acceleration in the horizontal direction. Hence,
$R = ut$
${v_1}t = {v_2}t.....\left( 1 \right)$ (Since ${R_1} = {R_2}$)
Time taken by the liquids coming out the holes at the points P and Q.
${t_1} = \dfrac{{\sqrt {2\left( {H - {h_1}} \right)} }}{g}$
${t_2} = \sqrt {\dfrac{{2{h_2}}}{g}} $
Where g is acceleration due to gravity.
Apply ${t_1}$ and ${t_2}$in$eq\left( 1 \right)$ we get,
$\left( {\sqrt {2g{h_1}} } \right)\left( {\dfrac{{\sqrt {2\left( {H - {h_1}} \right)} }}{g}} \right) = \sqrt {2g\left( {H - {h_1}} \right)} \sqrt {\dfrac{{2{h_2}}}{g}} $
We get,
$\left( {H - {h_1}} \right){h_1} = \left( {H - {h_1}} \right){h_2}$
Therefore \[{h_1} = {h_2}\]
$\dfrac{{{h_1}}}{{{h_2}}} = 1$

Hence option$\left( 1 \right)$ is the right option.

Note:Torricelli discovered the speed of efflux from an open tank is given by the formula identical to that of a freely falling body. Efflux means fluid outflow. Bernoulli’s equation applies to fluids with zero viscosity or non-viscous fluid. Bernoulli’s equation does not hold for turbulent flows, because in that situation velocity and pressure are constantly changing with time.