Question

In a class of 35 students, 17 have taken mathematics, 10 have taken mathematics but not economics. If each student has taken either mathematics or economics or both then the number of students who have taken economics bot not mathematics is:
(A)7
(B)25
(C)18
(D)32

Answer 1

Hint:Generally in these types of questions we will start with a Venn diagram and the term ‘AND’ is used for intersection and term ‘OR’ is used for union. Formula which we can use in these types of question is
$n\left( {M \cup E} \right) = n\left( M \right) + n\left( E \right) - n\left( {M \cap E} \right)$

Complete step-by-step answer:

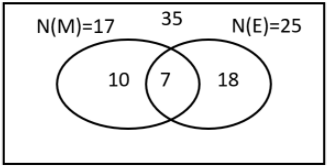
Number of total students = $35$
Number of students who taken mathematics = $n\left( M \right) = 17$
Number of students have taken mathematics but not economics = $n\left( {M \cap E'} \right) = 10$
$n\left( {M \cap E} \right) = $Number of students who have math and economics both.
So, according to question
$n\left( {M \cap E} \right) = n\left( M \right) - n\left( {M \cap E'} \right)$
$n\left( {M \cap E} \right) = 17 - 10$
$n\left( {M \cap E} \right) = 7$
$n\left( E \right) = $Number of students with economics.
$n\left( {M \cup E} \right) = $Number of students with maths or economics or we can say that total number of students
$n\left( {M \cup E} \right) = n\left( M \right) + n\left( E \right) - n\left( {M \cap E} \right)$
           $
  35 = 17 + n\left( E \right) - 7 \\
  n\left( E \right) = 42 - 17 \\
  n\left( E \right) = 25 \\
 $
So, the number of students who have taken economics is $25$.
$n\left( {E \cap M'} \right) = $Number of students with economics but not math’s.
$n\left( {E \cap M'} \right) = n\left( E \right) - n\left( {E \cup M'} \right)$
  $
  7 = 25 - n\left( {E \cup M'} \right) \\
  n\left( {E \cup M'} \right) = 25 - 7 \\
  n\left( {E \cup M'} \right) = 18 \\
 $
So, students who has taken economics but not mathematics is $18$
So the correct option is C.

Note:In these types of questions generally one can make mistakes in drawing a Venn diagram. So we careful while making that diagram and be careful about terms ‘AND’ and ‘OR’.