Question

In a class of 200 students who appeared for certain examinations. 35 students failed in MHT-CET. 40 in AIEEE and 40 in IIT entrance. 20 failed in MHT-CET and AIEEE. 17 in AIEEE and IIT entrance. 15 in MHT-CET and IIT entrance and 5 failed in all three examinations.
Find how many students.
a)did not fail in any examination.
b)failed in AIEEE or IIT entrance.

Answer 1

Hint: For solving this problem, first draw the Venn diagram of the situation by analysing the statement provided in the problem. Now we assign different values to different parts of the circle. By using this data representation, we can easily evaluate our answer.

Complete step-by-step answer:

A Venn diagram is a simple representation of data in the form of a circle having a quantified value. Venn diagrams, also called Set diagrams or Logic diagrams, are widely used in mathematics, statistics, logic, teaching, linguistics, computer science and business. It is very helpful to illustrate the relationships between the sets.

For, our case, the Venn diagram can be illustrated as:

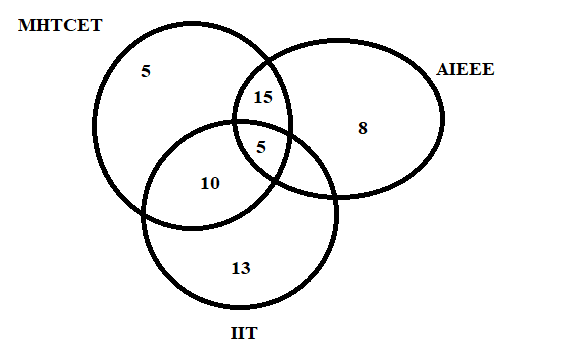
By observing the various sets, we get

Students failed in MHT-CET $=35$ students.

Students failed in AIEEE $=40$ students.

Students failed in IIT $=40$ students.

Students failed in MHE-CET and AIEEE $=20$ students.

Students failed in MHT-CET and IIT $=15$students.

Students failed in all entrance $=5$ students.

a)Students did not fail in any examination = Total number of students – total number of students fail in one or more entrances.

Students did not fail in any examination = 200 – 68 = 132 students.

b)Students failed in AIEEE or IIT is individual sum of students failed in AIEEE and IIT subtracted by the common students in both:

 $\begin{align}

  & =40+40-17 \\

 & =63 \\

\end{align}$

Hence, 63 students failed in one of the exams.

Note: The key concept for solving this problem is the knowledge of Venn diagrams. Venn diagram is a very helpful tool for analysing data. It helps the student to solve a problem without using any mathematical formulation.