Question

In a class, 54 students are good at Hindi only, 63 students are good at mathematics only, and 41 students are good at English only. There are 18 students who are good at both Hindi and Mathematics and 10 students are good at all three subjects. What is the number of students who are good in either Hindi or Mathematics but not in English?
(a) 99
(b) 107
(c) 125
(d) 130

Answer 1

Hint: We solve this problem by converting the given data into sets. There are three sets that are Hindi, Mathematics and English. We use the venn diagrams for all the sets and we find the required result using the venn diagram. The venn diagram of three combined sets can be shown as

Complete step by step answer:
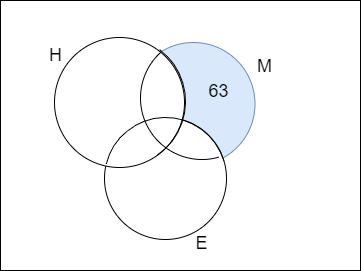
We are given that the number of students who are good at Mathematics only is 63
By converting the above statement in venn diagram we get

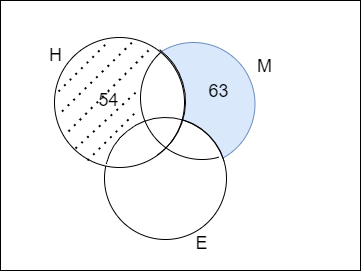
We are given that the number of students who are good at Hindi only is 54
By converting the above statement in venn diagram we get

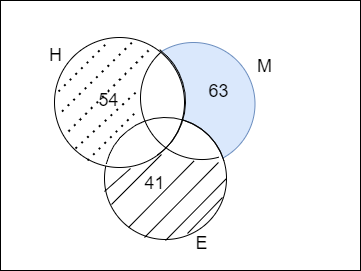
We are given that the number of students who are good at English only is 41
By converting the above statement in venn diagram we get

We are also given that there are 18 students who are good at both Hindi and Mathematics and 10 students are good at all three subjects
By converting the above statement in venn diagram we get

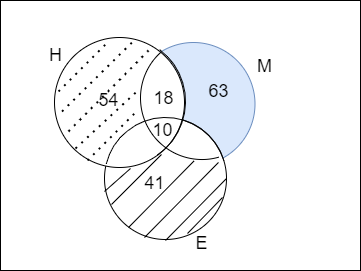
Now, we are asked to find the number of students who are good in either in Hindi or Mathematics but not in English


The venn diagram of the required part will be

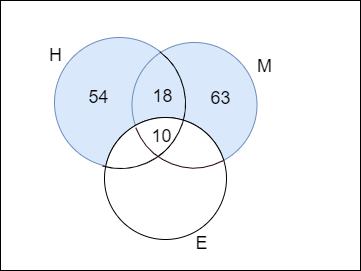
Let us assume that the number of students who are good in either in Hindi or Mathematics but not in English as \['N'\]
Here, from the venn diagram we can see that the number of students who are good in either in Hindi or Mathematics but not in English can be calculated as
\[\begin{align}
  & \Rightarrow N=54+63+18-10 \\
 & \Rightarrow N=125 \\
\end{align}\]
Therefore there are 125 students who are good in either Hindi or Mathematics but not in English.

So, the correct answer is “Option A”.

Note: Students may make mistakes in taking the number of students in each set.
We are given that the number of students who are good at Mathematics only is 63. Here, the term only refers to the venn diagram as shown below

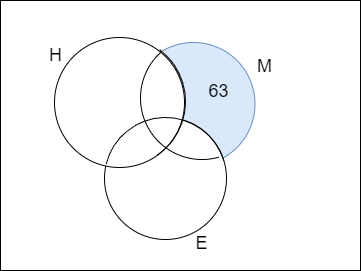
But students may take the count 63 whole mathematics set which will be wrong that is
\[\Rightarrow n\left( M \right)\ne 63\]
Similarly, we need to take care of remaining sets.